Implicitní funkce

Jsou situace, kdy nedostaneme funkci explicitně, ale pomocí rovnice, ve které se vyskytují jak neznámá, tak funkce. Například rovnice x + y = 1 definuje funkci danou vzorcem y = 1 − x, tj. f (x) = 1 − x. Není ale pravda, že bychom vždy dokázali vzít rovnici s x a y a změnit ji na funkci. Abychom viděli, co se může stát, uvažujme několik příkladů. Podíváme se na několik rovnic ve tvaru F(x,y) = c. Formálně takováto rovnice nedává funkci (alespoň ne okamžitě a vždy), ale popisuje množinu určitých bodů v rovině.

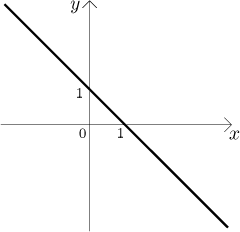
Příklad 1: Uvažujme rovnici   x + y = 1. Množina všech bodů v rovině, které ji splňují, je přímka:

Použili jsme známý fakt, že rovnice ve tvaru třeba ax + by = c dávají přímky. Jak už jsme viděli, množina daná touto rovnicí ve skutečnosti dává křivku, kterou lze také interpretovat jako graf jisté funkce.

Příklad 2: Uvažujme rovnici   y² = x. Množina všech bodů v rovině, které ji splňují, je následující:

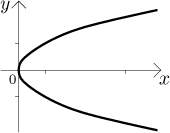
Abychom to zjistili, použili jsme jednoduchý trik, "prohodili" jsme proměnné a představili jsme si, že x závisí na y; rovnice pak popisuje základní parabolu, stačilo ji správně nakreslit (s prohozenými osami). Zase dostaneme křivku, tentokráte už ji ale nemůžeme považovat za graf nějaké funkce. Na druhou stranu je možné ji dostat jako spojení dvou grafů. Pokud vyřešíme danou rovnost pro y, dostaneme y = ±, což ukazuje, které dvě funkce dají celou křivku.

Příklad 3: Uvažujme rovnici

(|x| − 1)² + y² = 1.

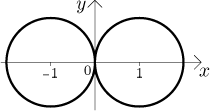
Abychom viděli tohle, použili jsme další trik. Pokud by x bylo v rovnici bez absolutní hodnoty, pak by rovnice popisovala kružnici s poloměrem 1 a středem (1,0) (viz níže). Přidání absolutní hodnoty kolem x znamená, že rovnici splňuje také tvar symetrický okolo osy y. Zase nelze vyjádřit tento tvar jako graf funkce, ale měli bychom být schopni jej dát dohromady jako dva grafy, ony dva kopce nad osou x jako jeden a dva kopce pod jako druhý. Všimněte si, že když dáme na pravou stranu rovnice číslo menší než 1, pak dostaneme dva kruhy, které jsou od sebe vzdáleny, takže už bychom ani neměli jednu nepřerušovanou křivku.

Příklad 4: Uvažujme rovnici

(|x| − 1)² + y² = 0.

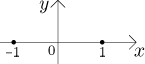
Tento příklad ukazuje, že rovnice nemusí dávat křivku. Zde máme dva body, dá se snadno napsat rovnice, která by vyjádřila dokonce nekonečně mnoho bodů, které jsou všechny izolované.

Příklad 5: Uvažujme rovnici

(|x| − 1)² + y² = −1.

Příklad 6: Uvažujme rovnici   sin(y) = x. Množina všech bodů roviny splňujících tuto rovnici vypadá takto:

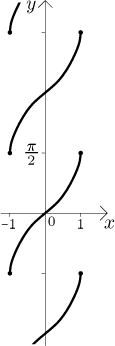
Tento příklad je docela zajímavý. Když zkusíme vyřešit danou rovnici pro y, vidíme, že existuje nekonečně mnoho řešení, funkce tvaru   y_k = arcsin(x) + 2πk pro všechna celá čísla k splňují tuto rovnici (viz Goniometrické funkce v části Funkce - Teorie - Elementární funkce). Obrázek tedy správně naznačuje, že množina daná rovnicí se skládá z nekonečně mnoha křivek, z nichž každou lze interpretovat jako graf funkce.

Pomocí těchto příkladů jsme chtěli ukázat, že rovnice mohou definovat velice podivné množiny v rovině, bylo by tedy naivní očekávat, že z nich vždycky dokážeme udělat funkci. Abychom do toho viděli lépe, podíváme se blíže na to, co je obvykle potřeba.

Problém: Máme rovnici s x a y. Máme také bod (x₀, y₀) splňující tuto rovnici. Chceme najít okolí U bodu x₀ a funkci y = y(x) na tomto okolí tak, aby y(x₀) = y₀ (tj. aby daný bod ležel na grafu této funkce) a aby pro všechna x z U platilo, že páry (x, y(x)) splňují danou rovnici (tj. graf této funkce souhlasí s množinou danou rovnicí na okolí daného bodu).

Připomeňme, že když zkoumáme funkce, potřebujeme okolí na to, abychom mohli hledat limity nebo derivaci, je tedy přirozené požadovat, abychom popsali křivku coby funkci na okolí daného bodu.

Zpět k Příkladu 2: Jestliže nám někdo dá bod (4,2), pak můžeme najít okolí bodu x₀ = 4, například U = (3,4.5), a funkci, jmenovitě y(x) = , která na U vlastně popisuje danou křivku okolo bodu (4,2).

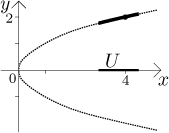
Jinými slovy, lokálně, na okolí daného bodu, jsme schopni vyřešit danou rovnici pro y. Podobně, pokud nám někdo dá bod (1,−1), pak můžeme najít okolí bodu x₀ = 1, například U = (0,2), a funkci, jmenovitě y(x) = −, která na U vlastně popisuje část křivky okolo (1,−1).

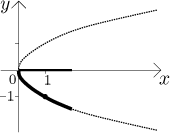
Zase jsme tedy schopni vyjádřit lokálně křivku jako funkci, ale jinou funkci než předtím. To je naprosto normální. Nakonec uvažujme bod (0,0). Zde máme smůlu. Jakkoli malé okolí zkusíme, vždy tam budou body x, pro které máme na křivce dvě různé hodnoty, proto nelze tuto křivku vyjádřit na okolí (0,0) jako funkci. Toto je, bohužel, také docela normální. Například v Příkladě 3 dokážeme tuto křivku vyjádřit lokálně všude kromě bodů (−2,0), (0,0) a (2,0).

To nám říká následující. Pokud máme křivku danou rovnicí, pak máme často šanci vyjádřit její části okolo daného bodu pomocí funkcí (zvaných implicitní funkce), ale někdy to není možné. Existuje způsob, jak rozeznat "dobré" body od "špatných"? Po pravdě řečeno, existuje, ale vyžaduje pokročilejší matematiku (funkce více proměnných, parciální derivace). Pro úplnost zde uvedeme příslušné tvrzení.

Věta (o implicitní funkci).
Uvažujme rovnici F(x, y) = c. Nechť bod (x₀, y₀) splňuje tuto rovnici. Jestliže

pak existuje okolí U bodu x₀ a funkce y = y(x) na tomto okolí taková, že y(x₀) = y₀ a F(x, y(x)) = c pro všechna x z U.

Příklad: Uvažujme křivku danou rovnicí   y³ + 1 = xy. Definuje implicitní funkci na nějakém okolí bodu (2,1)?

Řešení: Nejprve přepíšeme rovnici, aby vyhovovala vzorci z věty:

xy − y³ = 1.

Teď najdeme příslušnou parciální derivaci.

Protože je tato derivace nenulová, podle Věty o implicitní funkci existuje žádaná funkce na nějakém okolí x₀ = 2. Bohužel, nedokážeme ji rozumně najít. (Pro kořeny kubického polynomu sice máme vzorce, ale jsou hnusné a stejně si je nikdo nepamatuje.)

K čemu je tedy tohle všechno dobré? Za prvé, vidíme, že implicitní křivky jsou bohatší množina než množina možných "pěkných" grafů funkcí. Jinými slovy, implicitně lze popsat objekty, které by bylo obtížné popsat pomocí grafu funkcí (viz níže). To je výhoda implicitně definovaných křivek.

Na druhou stranu jestliže chceme takové křivky zkoumat (například hledat tečny), pak bychom s nimi mnohem raději pracovali jako s funkcemi. Ta věta výše něco říká, možná ne mnoho, ale všimněte si, že zrovna problém tečny je něco, kde stačí znát funkci lokálně. Co je ještě zajímavější, existuje způsob, jak najít derivaci implicitní funkce, aniž bychom znali její vzorec. To se může hodit, viz Implicitní derivování v části Derivace - Teorie - Implicitní a parametrické funkce.

Dva příklady práce s implicitními funkcemi na úrovni, kterou teď známe, lze najít v Řešených příkladech.

Poslední poznámka: Mluvili jsme o změně implicitních křivek ve funkce. Dá se to také udělat naopak? Odpověď je kladná a je to tak snadné, že na to nebudeme plýtvat dalším odstavcem. Je-li křivka dána jako graf funkce y = f (x), můžeme to vždy vyjádřit pomocí implicitní rovnice y − f (x) = 0. Mohli bychom samozřejmě zkusit něco jiného, třeba 2y − 2f (x) + 2 = 2, můžeme vlastně takový graf vyjádřit nekonečně mnoha způsoby jako implicitní křivku. A to je všechno.

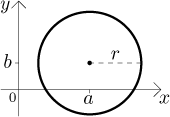
Bonus: Pár slavných křivek.

Elipsa s hlavní poloosou A, vedlejší poloosou B a středem (a,b) je dána rovnicí

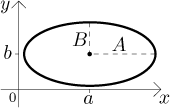
Je evidentní, že když vezmeme A = B = r, dostaneme kružnici.

Parametrické funkce
Zpět na Teorie - Implicitní a parametrické funkce