Definice.
Nechť f má primitivní funkci F na intervalu I, kde
I je interval
libovolného druhu od a do b. Pak definujeme Newtonův určitý
integrál z f
od a do b jako
![]()
Pokud tato limita existuje konečná, řekneme, že daný integrál konverguje.
To, že mnohé funkce nejsou Riemannovsky integrovatelné, inspirovalo zavedení jiných druhů určitého integrálu. Dnes se již jedná o velmi bohatou oblast bádání. My se zde jen krátce podíváme na dvě populárnější a intuitivně jednodušší definice určitého integrálu.
Definice.
Nechť f má primitivní funkci F na intervalu I, kde I je interval libovolného druhu od a do b. Pak definujeme Newtonův určitý integrál z f od a do b jako
Pokud tato limita existuje konečná, řekneme, že daný integrál konverguje.
Tato definice je zapsána takto obecně, aby jí šlo použít i pro jiné intervaly než uzavřené, dokonce funguje i pro intervaly, jejichž koncové body mohou být nekonečno, pak vlastně dostaneme neurčitý integrál (cf. zde).
Pro nás je ovšem nejpřirozenější situace, když je F primitivní funkcí
k f na
![]()
Ze Základní věty integrálního počtu okamžitě obdržíme
Důsledek.
Pokud je f Riemannovsky integrovatelná a Newtonovsky integrovatelná na⟨a,b⟩, pak tyto dva určité integrály souhlasí.
Je to jednoduché, dostáváme pak totiž přesně Newton-Leibnizovu formuli.
Povšimněte si, že obecně tyto dva pojmy nemusí souhlasit. Příklad skokové funkce ukazuje, že existují funkce, které jsou Riemannovsky integrovatelné ale ne Newtonovsky integrovatelné. Existují také funkce, které jsou Newtonovsky integrovatelné, ale ne Riemannovsky integrovatelné.
Nepodáme zde přesnou definici, protože ta potřebuje docela pokročilou matematiku. Proto jen naznačíme hlavní myšlenku.
Když jsme definovali Riemannův integrál funkce f, rozdělili jsme oblast pod grafem f na svislé pruhy dané dělením osy x. Lebesgueův integrál to dělá jinak: rozdělí danou oblast na svislé pruhy dané dělením osy y.
Zvolme nějakou hodnotu y a uvažujme velice tenký vodorovný proužek na
úrovni y. Pokud protne graf funkce f, podíváme se na množinu
B všech bodů x, pro které
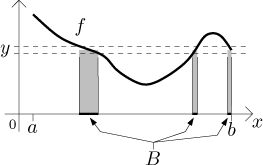
Teď se podívejme na oblast pod těmi částmi grafu f, které leží v daném
proužku (šrafovaná oblast). Pokud dokážeme nějak změřit velikost množiny
B, pak obsah této šrafované oblasti je roven y krát velikost
B. Velikost množiny se dá měřit mnoha způsoby. Lebesgueův integrál
používá způsob zvaný Lebesgueova míra a je příliš složitý na to,
abychom jej tady popsali. Lebesgueova míra je docela přirozená, například
Lebesgueova míra intervalu
Měření množin je hlavním problémem tohoto přístupu. Pokud je daná funkce velmi divoká, pak množiny B mohou být velmi podivné a nemusíme být schopni je změřit. Nicméně Lebesgueova míra je velmi mocná a pokud je daná funkce alespoň trochu pěkná, dokážeme změřit množiny odvozené od všech hodnot y. Poznamenejme, že pokud vodorovný pruh na úrovni y neprotne graf f, je odpovídající množina B prázdná a má míru nula.
Z obrázku by se zdálo, že pokud se podíváme na výše popsané šrafované oblasti příslušející různým hodnotám y, jde o disjunktní množiny:
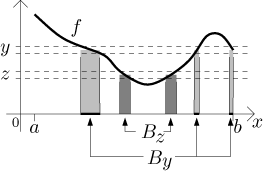
Celková plocha pod grafem je tedy rovna součtu obsahů takových oblastí:
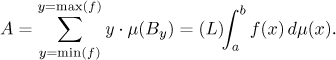
Tomuto se říká Lebesgueův integrál funkce f.
Protože je definice velmi složitá, dá se čekat, že pojem Lebesgueova integrálu je velmi silný. A taky že ano, dá se použít i pro velmi podivné funkce, dokonce i pro Dirichletovu funkci, která není Riemannovsky ani Newtonovsky integrovatelná. Dá se dokázat, že Lebesgueův integrál této funkce přes libovolný interval je roven nule. Pomocí Lebesgueova integrálu také můžeme integrovat přes jiné množiny, než jsou intervaly.
Aby měly věci smysl, nové pojmy určitého integrálu by neměly být v rozporu s těmi obvyklými. A to také platí, pro "pěkné" funkce hodnoty jejich Lebesgueových integrálů souhlasí s Riemannovými a Newtonovými určitými integrály. Kupříkladu pokud je f spojitá, pak je integrovatelná všemi popsanými způsoby a
![]()