Definice.
Nechť a je reálné číslo, nechť
![]()
za předpokladu, že limita konverguje. Pak řekneme, že dotyčný nevlastní integrál konverguje.
Pokud limita nekonverguje, řekneme, že daný nevlastní integrál diverguje.
Když jsme definovali určitý (Riemannův) integrál na uzavřeném intervalu I, měli jsme na integrovanou funkci dva hlavní požadavky: aby byla definovaná a omezená na celém uzavřeném intervalu I. (Připoměňme, že tyto podmínky ještě nezaručují, že funkce bude Riemannovsky integrovatelná).
Teď se tuto definici pokusíme rozšířit na obecnější případy. V zásadě se mohou pokazit dvě věci. Jednak může být jeden či oba koncové body intervalu I nekonečné (pak přirozeně nelze uvažovat uzavřený interval), druhak nemusí být funkce definovaná či omezená na I. Nejjednodušší případ je ten, kdy se něco špatného stane v jednom z koncových bodů I. V následující definici se vypořádáme s případem, že se něco podezřelého děje v pravém koncovém bodě:
Definice.
Nechť a je reálné číslo, nechťb > a je reálné číslo nebob = ∞. Nechť f je funkce Riemannovsky integrovatelná na intervalech⟨a,B⟩ pro všechna B z(a,b). Pak definujeme nevlastní Riemannův integrál z f od a do b jako
za předpokladu, že limita konverguje. Pak řekneme, že dotyčný nevlastní integrál konverguje.
Pokud limita nekonverguje, řekneme, že daný nevlastní integrál diverguje.
Abychom pochopili smysl této definice, podíváme se na dva typické případy "špatných pravých koncových bodů". Na prvním obrázku funkce "vybouchne" v b, na druhém obrázku interval utíká do nekonečna:
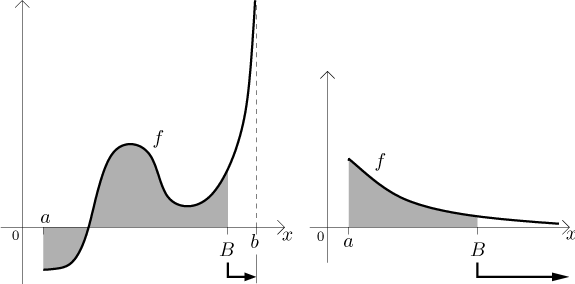
V obou případech se dokážeme "špatnému konci" vyhnout tím, že ho
odřízneme - použijeme pro to odřezávacího bodu B. Na intervalu
Připomeňme, že pro výpočet určitých integrálů dáváme přednost použití
primitivních funkcí (Newton-Leibnizova formule). Jinými slovy, předpoklad
ohledně Riemannovské integrovatelnosti v definici je sice dobrý pro teorii,
ale my bychom spíš ocenili, kdyby daná funkce také splňovala předpoklady
Základní věty integrálního
počtu. Nejpřirozenější požadavek je, aby f byla spojitá na všech
intervalech
"Problém" se také může vyskytnout na levém konci:
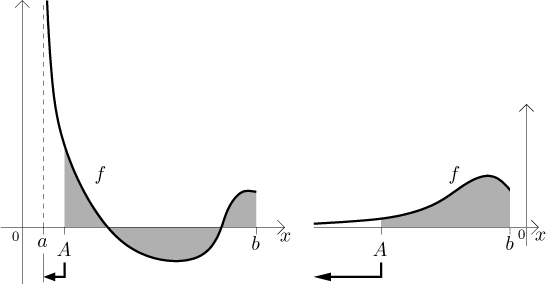
Příslušná definice je teď už asi jasná:
Definice.
Nechť a je reálné číslo neboa = −∞, nechťb > a je reálné číslo. Nechť f je funkce Riemannovsky integrovatelná na intervalech⟨A,b⟩ pro všechna A z(a,b). Pak definujeme nevlastní Riemannův integrál z f od a do b jako
za předpokladu, že limita konverguje. Pak řekneme, že dotyčný nevlastní integrál konverguje.
Pokud limita nekonverguje, řekneme, že daný nevlastní integrál diverguje.
I zde obvykle nepoužíváme předpoklady, jak jsou napsány, ale doufáme v něco
víc: Zde bychom v praxi chtěli, aby f byla spojitá na
Tyto dvě definice ukazují přesně, jak počítat nevlastní integrály tohoto základního typu, není třeba nějaké speciální metody.
Příklad: Vypočítejte (pokud konverguje)
![]()
Zde máme evidentně problém v nekonečnu, tj. v pravém koncovém bodě. Pokud budeme integrovat pouze až do nějakého čísla (většího než 1), funkce tam bude spojitá a tudíž i Riemannovsky integrovatelná, žádné další problémy nejsou. Můžeme tedy použít první definici:
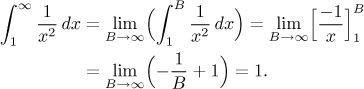
Integrál tedy konverguje.
Všimněte si, že to vlastně znamená toto: Pokud se podíváme na graf této funkce,
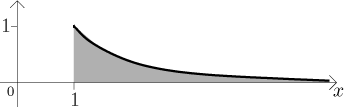
vidíme, že oblast pod grafem není ohraničená, pokračuje doprava, aniž by skončila. Přesto má konečný obsah. Důvodem je, že graf se blíží k ose x velice rychle, takže jak postupujeme doprava, přírůstky k obsahu se nenasčítají do nekonečna (dokonce ani do velkého čísla, jak jsme viděli). Je tu souvislost s faktem, že pokud se čísla zmenšují dostatečně rychle, pak jich můžeme sečíst nekonečně mnoho a dostat rozumný výsledek (cf. geometrická řada).
Naopak funkce, které v nekonečnu nejdou k nule dostatečně rychle, mohou mít nekonečnou plochu pod grafem (jinými slovy, takový integrál by divergoval). Obrázek by vás pak měl přesvědčit, že pokud funkce konverguje v nekonečnu k nenulovému číslu (či nekonečnu), pak integrál do nekonečna musí divergovat (protože obsah bude zjevně nekonečný). Takže například

Viděli jsme příklad konvergentního integrálu. Pokud se chcete podívat, co se může pokazit a co může způsobit, že integrál diverguje, podívejte se sem.
Důležitá poznámka: Co se stane, pokud tuto proceduru použijeme na vlastní Riemannův integrál? Přesně řečeno, co když je f Riemannovsky integrovatelná na uzavřeném intervalu I a my aplikujeme onu proceduru "odřízni a zalimiť" na některý z koncových bodů? Dostaneme správnou odpověď. To plyne z věty o limitních vlastnostech Riemannova integrálu. Vyplývá z toho, že naše definice nevlastního integrálu zobecňuje obvyklý Riemannův integrál.
Teď zadefinujeme obecnější případ, zobecněný Riemannův integrál. Budeme předpokládat, že zkoušíme integrovat funkci f na nějakém intervalu I a vyskytují se tam "špatná místa", která nevyhovují výše popsané základní situaci; tedy je tam takových míst víc než jedno nebo se vyskytují uprostřed intervalu I.
Protože by určitý integrál měl být aditivní (obsah disjunktního sjednocení oblastí by se měl rovnat součtu obsahů jednotlivých oblastí), prostě daný integrál rozdělíme na několik "menších", aby každý z nich měl jen jeden "problém", a to na některém z koncových bodů. Na následujícím obrázku vidíme tři problémy, v bodech b, d a v nekonečnu. Abychom měli jen jeden problém v menších integrálech, potřebujeme zvolit nějaké dělící body (v tomto příkladě c a e) a pak uvažovat pět integrálů, každý z nich bude mít jen jeden problém v nějakém koncovém bodě. Proto je můžeme vypočítat pomocí již známých definic:
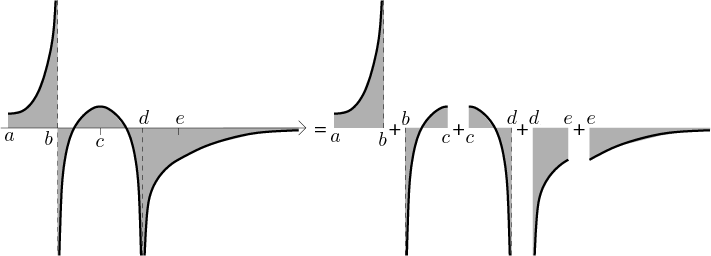
Formálně:
Definice.
Nechť a je reálné číslo neboa = −∞, nechťb > a je reálné číslo nebob = ∞. Nechť f je funkce definovaná na(a,b) s možnou výjimkou konečně mnoha bodů. Předpokládejme, že existují bodya = x0 < x1 < . . . < xn−1 < xn = b takové, že všechny integrály
jsou nevlastní integrály ve smyslu předchozích definic. Pak definujeme zobecněný Riemannův integrál jako
za předpokladu, že všechny integrály v součtu konvergují. Pak řekneme, že daný (zobecněný) Riemannův integrál z f od a do b konverguje.
Pokud jeden či více integrálů v součtu divergují, řekneme, že daný integrál z f od a do b diverguje.
Pokud integrál konverguje či pokud má výraz v sumě smysl, pak řekneme, že integrál z f od a do b existuje. Jinak řekneme, že neexistuje.
Integrá, který existuje, může buď konvergovat, nebo být nekonečno či mínus
nekonečno. Neexistuje, pokud při rozkladu jako v definici dojdeme k
neurčitému výrazu
Jinak řečeno, integrál, který diverguje, může divergovat pěkně (když je
obsah roven nekonečnu nebo mínus nekonečnu, což není pěkné ale pořád to něco
říká), nebo škaredě (když jsou v obsahu zapletena opačná nekonečna).
Tato definice nám zase dává rovnou návod k výpočtu zobecněného Riemannova integrálu.
Příklad: Vypočítejte (pokud konverguje)
![]()
Jak vidíme, jsou tam dva problémy, jmenovitě když
![]()
A teď počítáme:
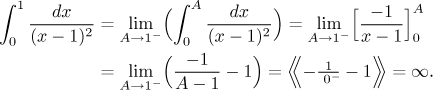
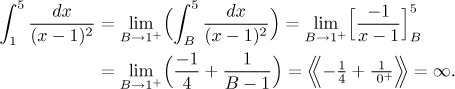
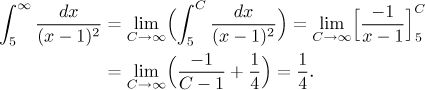
Protože některé z těchto integrálů jsou divergentní, také celý daný integrál diverguje. Popravdě řečeno, když nám ten první vypočtený integrál nekonvergoval, mohli jsme hned skončit a prohlásit, že integrál od 0 do ∞ je divergentní - ty další dva už to nemohly zachránit. Nicméně jsme je spočítali a tak už víme, že tento integrál sice diverguje, ale pěkně, daný integrál existuje. Zapíšeme to takto:
![]()
Celá procedura se dá vyjádřit následujícím obrázkem:
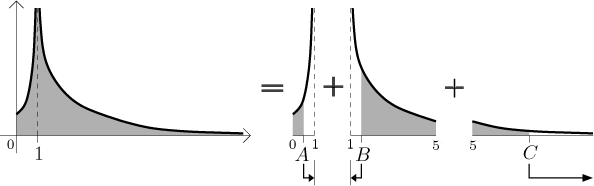
Všimněte si, že první dvě oblasti, které utíkaly bez omezení nahoru, nakonec měly nekonečný obsah. To neplatí nutně pro všechny funkce se svislou asymptotou. Jestliže se graf funkce přimyká ke svislé asymptotě rychleji než náš příklad ("tiskne se" k ní), pak příslušná neomezená oblast může mít konečný obsah. Zde odkážeme na příklad v následující sekci.
Měli bychom poznamenat, že zase počítáme ty menší integrály přes primitivní funkce, takže naše poznámka o spojitosti (coby nejsnažší cestě k Newton-Leibnizově formuli) ze začátku pořád platí. Když nám tedy někdo dá integrál od a do b, vždy musíme prozkoumat tento uzavřený interval a hledat problémy dvou druhů: body, kde f není definovaná, a body, kde není spojitá. Připomeňme, že funkce spojitá na omezeném uzavřeném intervalu musí být omezená (viz Spojitost v části Funkce - Teorie - Reálné funkce). Znamená to, že když se díváme po problémech se spojitostí, tak zároveň i najdeme problémy s omezeností f. Proto během hledání problémů s definicí a spojitostí najdeme všechny možné problémy; jinými slovy, je to matematicky korektní.
Důležitá poznámka: Výpočet nevlastních integrálů přes primitivní funkce v sobě skrývá past. Mnohé primitivní funkce jsou nalezeny pomocí metod, které jako výsledek dají součet členů. Je naprosto nutné aplikovat příslušnou limitu na celý výsledek. Pokud to neuděláme, můžeme dostat neurčitý výraz, ačkoliv zadaný nevlastní integrál může konvergovat.
Podívejme se na následující příklad: Uvažujme konstantní funkci
![]()
Do průšvihu se dostaneme, pokud se pokusíme tuto primitivní funkci použít v nevlastním integrálu od 0 do nekonečna a podlehneme pokušení rozdělit limitu na dvě:
![]()
Dostali jsme rozdíl dvou nekonečen, což je neurčitý výraz. Protože limity divergují, je teď lákavé prohlásit, že nevlastní integrál je divergentní. To by ale byl nesprávný závěr. Nekonečna v našem výsledku nejsou součástí problému (plocha pod grafem f ), pouze výsledek našeho nešikovného zacházení s primitivní funkcí. Pokud bychom limitu nerozdělili na dvě, nekonečna by nevznikla:
![]()
Teď asi máte pocit, že byste takovou hloupou chybu nikdy neudělali, ale stejný problém může nastat například při integraci používající rozklad na parciální zlomky. Pak se může zdát přirozené aplikovat limitu na každý parciální zlomek zvlášť, a už je tu zase stejný problém. Je proto nezbytné vždy držet primitivní funkci pohromadě a aplikovat limitu na celý výraz.
Všimněte si, že tento problém je ve své podstatě odlišný od procedury, kdy jsme integrál rozdělovali na několik menších, abychom zajistili, že v každém bude jen jeden problematický bod. V tomto případě totiž děláme něco, co odpovídá geometrickému rozdělování oblasti na menší části. Pokud pak zjistíme, že jedna z částí nemá konečný obsah, celá oblast je "špatná" a už se to nedá spravit. I kdyby tam ještě byla jiná část se stejně nekonečným obsahem, ale s opačným znaménkem, nekonečna by se nekrátila; jakmile je oblast někde "patná", je prostě "špatná". Ten problém s primitivní funkcí je něco úplně jiného. Pokud vyjádříme primitivní funkci jako součet členů, nemá to nic společného s oblastmi a za problémy, které se mohou vyskytnout, si můžeme sami. Pokusíme se to blíže osvětlit v Řešených příkladech.
Způsob, kterým tady počítáme nevlastní integrály, není zrovna nejpohodlnější. Pokud se podíváte na příklady výše i v dalších sekcích, možná si všimnete, že vlastně integrály počítáme jako obvykle, jen na konci namísto dosazování děláme u problémových mezí integrace limitu. Z toho vychází obvyklý způsob zápisu, který si ukážeme na integrálu počítaném výše
![]()
Je to výrazně kratší než postup přesně podle definice, nicméně stále korektní, pokud zachováváme základní pravidlo: V integrálu, který takto počítáme, je povolen nejvýše jeden problémový koncový bod, a ten dosazujeme limitou z vhodné strany. V praktických částech Math Tutoru budeme samozřejmě používat tento příjemný způsob, zde v teoretické části ještě zůstaneme u toho z definice, protože přesně vyjadřuje podstatu neučitého integrálu, tudíž nám pomůže s chápáním věcí okolo.