Integrace per partes

Metoda je založena na této matematické větě. Vzorec z věty

nám říká, jak počítat. Co vidíme? Výraz v integrálu, který počítáme, si zapíšeme jako součin (pokud je to možné, to je první omezení metody). Jeden činitel si označíme jako f (x), druhý jako g′(x). Vzorec říká, že místo daného integrálu je možné vzít výraz napravo. Na to ale musíme znát dvě další věci, jmenovitě f ′(x), což obdržíme derivováním funkce f (x), a g(x), což získáme z funkce g′(x) integrováním. Všimněte si, že za g nemusíme brát celý neurčitý integrál včetně "+C", stačí nějaká primitivní funkce, která se nám líbí (obvykle ta nejjednodušší).

Nový výraz na pravé straně již budeme při třoše štěstí (tedy při správné volbě f a g) umět udělat. Typický příklad, na kterém také ukážeme typický zápis per-partes:

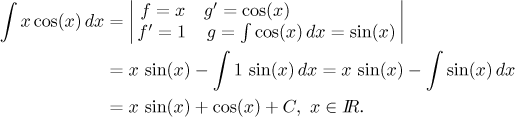
Poznamenejme, že různí autoři volí různé značení, někteří mají také f a g, ale derivace naopak (nalevo se derivuje g, napravo f ), jiní volí jiná písmenka (populární jsou třeba u a v) a dokonce existuje verze s diferenciály:

Předchozí příklad by pak šel

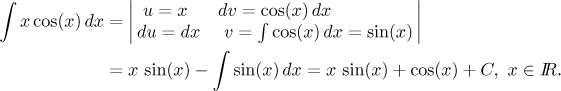
Na tom, který konkrétní vzorec použijete, samozřejmě nezáleží, vyberte si dle libosti. Já mám trochu slabost pro ten s diferenciály, ale mám pocit, že ten prvně použitý se potkává nejčastěji, tak se jej budeme v Math Tutoru držet. Ve skutečnosti zkušení integrátoři nepoužívají vzorce vůbec. Prostě v daném integrálu jednu část integrují, čímž dostanou ten prostřední člen, a pak druhou zderivují, dostanou tak výraz do nového integrálu.

Jaká jsou omezení této metody? Je jasné, že nulze nasadit na integrál z výrazu, který není součin. Ale i když součin máme, ječště není vyhráno. Ty hlavní problémy ukážeme na následujícím příkladě.

Zkusíme podobnou volbu jako předtím.

Dostali jsme pro g integrál, který neumíme metodami pokrytými v Math Tutoru vyřešit, ve skutečnosti je to hodně drsný integrál. Toto je tedy první faktor: Když vybíráme kandidáty pro f a g′(x), tak bychom měli myslet na to, že musíme být schopni zvolené g′(x) snadno integrovat. To bude určitě pravda, když naši volbu prohodíme.

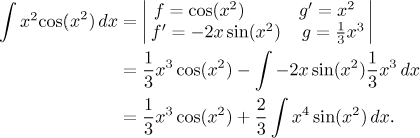
Teď se integrování per partes povedlo, ale nový integrál je dokonce ještě horší než ten původní. Takže to sice fungovalo, ale bylo to k ničemu. To je tedy druhá věc, kterou je třeba mít na paměti, když přemýšlíme nad integrací per partes. Tento integrál mimochodem pomocí per partes vyřešit nejde.

Zkušení integrátoři vědí, že některé typy integrálů jsou přímo stvořeny pro integraci per partes. Pro praktické tipy viz Integrace per partes v části Přehled metod - Metody integrace.

Mimochodem, "per partes" znamená "po částech".

Je to v zásadě stejné jako integrování per partes v neurčitém integrálu. Nový integrál bude přirozeně také určitý se stejnými mezemi a ta část uprostřed je už vlastně hotová část primitivní funkce, takže ji použijeme k vyčíslení podle Newton-Leibnizova vzorce.

Pro jednoduchý příklad se vrátíme k prvnímu příkladu výše.

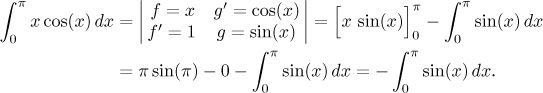
Zbytek je snadný.

Další sekce: parciální zlomky
Zpět na Teorie - Metody integrace