Příklad: Vypočítejte integrál

Řešení: Tento integrál se bude řešit nějakým trikem ze šuplíku "goniometrické integrály". Žádný pěkný ale nezabere, protože nám v čitateli chybí nějaká doplňující část k substituci. Ideální by bylo y = 1 + sin(x), na to bychom ale museli mít v čitateli kosinus. Šlo by to sice algebraicky zařídit, ale vzniklý integrál bude dost nepěkný, jak se můžete přesvědčit zde.

Zdá se tedy, že nezbývá nic jiného, než nasadit univerzální substituci pro goniometrický integrál (viz goniometrické integrály) v Přehledu metod - Integrace

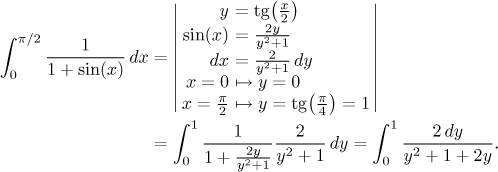
Tohle vypadá na parciální zlomky, ale když upravíme jmenovatel, ukáže se, že integrál udolá jednoduchá lineární substituce, neboť už to vlastně je parciální zlomek:

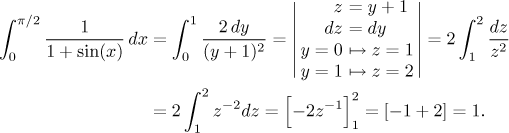
Nebylo to tedy až tak hrozné. Pokud bychom potřebovali integrál neurčitý, dostali bychom

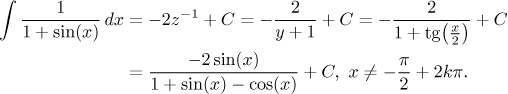
Poslední úprava a zkouška jsou naznačeny zde. Problém je s definičním oborem. Integrál existuje, pokud je jmenovatel nenulový; proto můžeme integrovat jen přes intervaly neobsahující body specifikované ve výsledku (s naším integrálem jsme tedy měli štěstí). Při výpočtu jsme ale prováděli substituci, která díky tangensu rovněž nepovoluje žádné celé násobky π. Co s tím? Tyto body během výpočtu zase přestaly "zlobit" a výraz, který vyšel, je v těchto bodech definován. Znamená to, že je to v pořádku? Matematicky ne, je to ovšem znamení, že máme velkou naději, že to nakonec dobře dopadlo. Zkouška ukázala, ža ano, "špatné body ze substituce" se tedy nakonec nějak "udobřily". Není to však pravidlem! Tento i tento příklad ukazují, že se na to nedá spoléhat.

Pro tento konkrétní integrál lze použít ještě jinou fintu, která nás může napadnout, když si vzpomeneme, že jedna z populárních goniometrických identit obsahuje výraz 1 + cos(t).

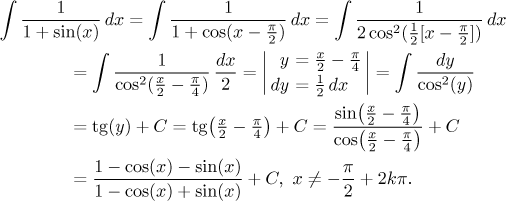
Poslední úprava i zkouška opět potřebují trochu zacvičit s goniometrickými identitami, postup je podobný jako u předchozího řešení tohoto příkladu.

Další příklad
Zpět na Řešené příklady - Integrace