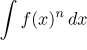Šuplík "goniometrické integrály"

Začneme pohledem na goniometrické integrály. Pokud jste sem přišli za hyperbolickými funkcemi, podívejte se na poznámku na konci.

Integrály s goniometrickými funkcemi jsou časté a na mnohé z nich existují standardní triky, mnohé jsou také v tabulkách. V zásadě se dá říct, že si člověk vystačí se znalostí, jak integrovat kombinace sinů a kosinů, protože všechny ostatní funkce se na ně dají převést. Někdy ale vznikají odporné věci, proto se budeme zabývat i některými populárnějšími kombinacemi tangensů a kotangensů. A protože inženýři ještě občas používají sekans a kosekans, podíváme se trochu i na ně. Jako poslední šanci si necháme univerzální substituci. Protože obecné postupy řešení bývají většinou pracné, podíváme se nejprve na typy, pro které existují pohodlnější postupy.

 • Typ 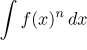, kde f je nějaká goniometrická funkce a n je kladné celé číslo. Obecně pro tyto integrály existují redukční vzorce, které platí pro přirozená čísla n větší nebo rovno 2:

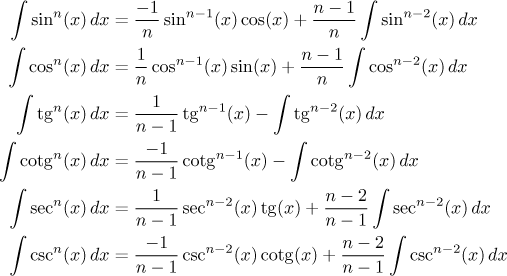
Všechny tyto výsledky se odvodí pomocí goniometrických vzorců a integrace per partes, můžete se podívat sem. Ještě poznámku k užitečnosti sekansů a kosekansů: Redukční vzorce platí jen pro kladná n! Znamená to, že pokud máte sinus nebo kosinus ve jmenovateli a v kladné mocnině, musíte použít vzorce pro sekans a kosekans.

Vzhledem k tomu, že při každém použití redukčního vzorce se mocnina v integrálu sníží o dvě, jsou dvě možnosti:

1. Pokud je n sudé, příslušná goniometrická funkce nakonec vymizí a my máme integrovat jedničku. Příklad:

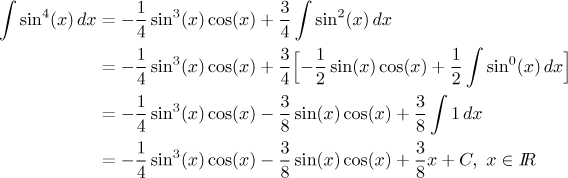
2. Pokud je n liché, zůstane nám nakonec integrál ze samotné goniometrické funkce. Integrál ze sinu a kosinu je tabulkový integrál a nečekáme žádné potíže. Příklad:

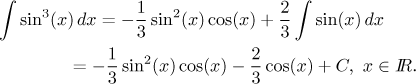
Teď se podívejme na ostatní čtyři goniometrické funkce, začneme tangensem:

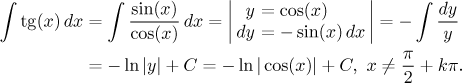
Tento výsledek je také možno upravit na tvar

Podobně integrujeme kotangens, což už jsme viděli v části Teorie - Metody integrace - Substituce.

Funkce sekans a kosekans jsou zřídka k vidění jako takové, nicméně reciproký kosinus a sinus se objevují často. Jejich integrály jsou trochu těžší, zahrnují trik typu přičtu-odečtu (v tomto případě spíš vynásobím-vydělím), substituci a parciální zlomky:

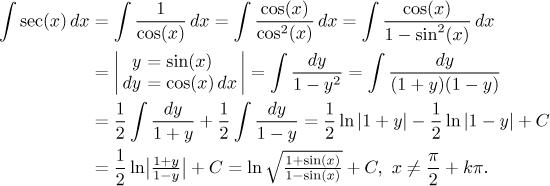
Alternativní výpočet, vhodný pro ty, kteří jsou dobře obeznámení se sekansy a kosekansy, je zde.

Protože výpočet pro kosekans je podobný, uvedeme pouze výsledek:

Poznámka: Při integrování reciprokých funkcí je dobré mít na paměti, že druhá mocnina ve jmenovateli znamená tabulkový integrál:

Důležitá poznámka: Pokud integrujeme lichou mocninu sinu či kosinu, můžeme si všechnu tu redukční práci odpustit. V tomto případě stačí "oddělit" jednu mocninu, která poslouží při substituci, zbývající (je jich teď na sudou mocninu) se převedou na komplementární funkci. Nejlépe je to vidět na příkladě:

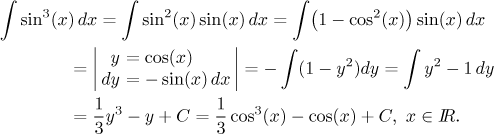
Všimněte si, že pokud je n sudé, pak se nám podobný substituční trik prostě nepovede. Právě přítomnost "extra sinu" či "extra kosinu" umožňuje substituci - a je jasným znamením, že ji máme použít. Konec konců, už jsme to viděli při integrování tangensu a sekansu. Všimněte si, že u sekansu se tento "extra kosinus" vyskytoval ve jmenovateli, ale nám to nevadilo, protože jsme si jej lehce převedli do čitatele.

Další alternativa - někdy velice účinná - je redukovat mocninu pomocí goniometrických identit. Dostáváme se tím k dalšímu typu, kde se na tento přístup podíváme blíže.

 • Typ 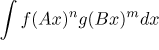, kde funkce f a g jsou siny nebo kosiny.

Tyto integrály se nejlépe řeší pomocí goniometrických identit. Obvykle nejlépe funguje, pokud nejprve zredukujeme mocniny pomocí

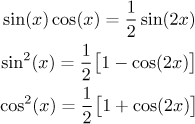
Tradičně se začne likvidací všechn možných součinů sin(Ax)cos(Ax) pomocí první formulky a pak se použijí další dvě na všechny zbylé mocniny. Zhruba řečeno, tyto formulky umožňují snížit mocninu na polovinu výměnou za zdvojnásobení argumentu.

Nakonec nám zbydou součiny ve tvaru f (Ax)g(Bx), kde A ≠ B, takže ty vzorce nahoře nezaberou. Naštěstí máme ještě další vzorce právě na tento případ:

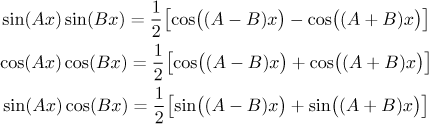
Příklad:

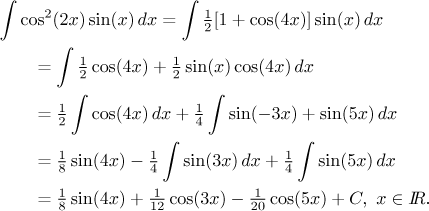
Existuje ovšem ještě opačná strategie, naopak se snažit pomocí vzorců o odstranění násobku u proměnné, většinou výměnou za mocniny, čímž obecně vzniká lineární kombinace integrálů s výrazy sin^m(x)cosⁿ(x), což zní lákavě. Nevýhoda tohoto postupu je, že není jasné, zda to dopadne dobře či ne. Předchozí postup vždy vede k integrálům, které lze snadno udělat lineární substitucí, u tohoto postupu je to loterie, protože je třeba použít postupy z dalšího typu níže.

Pokud je jedno z čísel m, n sudé a druhé liché, pak je relativně snadné takový výraz integrovat substitucí, viz první možnost níže. Ostatní možnosti (dvě sudé, dvě liché) jsou naopak tak komplikované, že první doporučovaný postup bývá lepší. Pokud tento alternativní postup zkusíme na našem posledním příkladě, tak se ukáže, že máme ohromné štěstí a integrujeme snadno pomocí "extra kosinu".

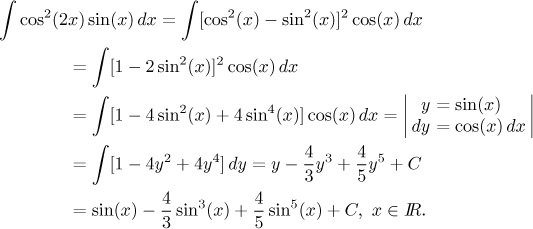
Poučení je, že zde sice probíráme jakési standardní postupy, ale dobrá znalost identit často nabídne lepší možnosti a goniometrické integrály bývají dost individuální.

Pro další příklad se vrátíme ke čtvrté mocnině sinu, který jsme výše řešili redukčními vzorci a zde se můžete podívat, jak se dá vyřešit pomocí identit. Metoda využívající goniometrických vzorců ale dokáže být občas mučení zvířátek, přesvědčit se můžete tady.

 • Typ 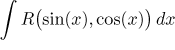, kde R je racionální lomená funkce dvou proměnných. Tento typ integrálu se vhodnou substitucí převádí na integrál z racionální lomené funkce, na který se pak standardně nasadí parciální zlomky a dál už víme, jak to dokončit. Tato kategorie nezahrnuje přímo integrály, kde argumenty sinu/kosinu jsou násobeny. Nicméně je možno použít goniometrických vzorců k úpravě výrazů typu sin(Ax) a cos(Ax), kde A je celé číslo, aby se to A ztratilo, takže snad všechny rozumné goniometrické integrály (včetně typů probraných výše) sem zapadají a vyplatí se umět s nimi zacházet.

Pro tento typ existuje standardní substituce, ta je ale dost pracná, tak se nejprve podívejme na dva případy, které jdou pěkněji:

1. Nejjednodušší je případ, kdy se v čitateli (či jmenovateli!) vyskytuje "extra sin" nebo "extra cos", na ostatních místech integrandu se vyskytují v sudých mocninách. Postupujeme pak již známým způsobem, který už jsme viděli, když jsme integrovali sekans či tangens; ukážeme si ještě jeden příklad:

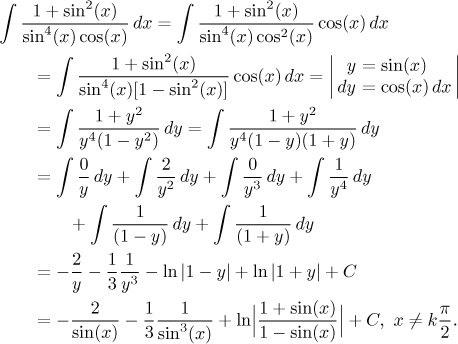
Méně často se povede podobný trik s tangensem: Pokud se nám podaří upravit výraz tak, aby tam byly jen tangensy a extra kosinus na druhou ve jmenovateli, projde substituce y = tg(x). Podobně zabere kotangensová substituce, pokud ve jmenovateli "vybydou dva siny" a zbytek se podaří napsat pomocí kotangensů.

2. Pokud se v integrálu vyskytují siny i kosiny v sudých mocninách, nemůžeme si jeden z nich vypůjčit k substituci. V takovém případě se dá použít triková substituce y = tg(x). Odtud se dají spočítat další funkce. U sinu si to naznačíme, kosinus se dělá podobně:

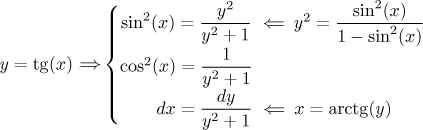
Teď je vidět, proč by tato substituce nefungovala, kdyby se vyskytovaly liché mocniny. Ukážeme ji na nějakém vhodném příkladě:

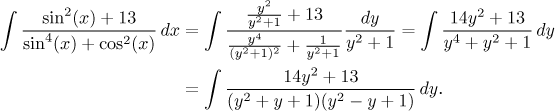
Příklad zase dokončí parciální zlomky, nástin řešení je zde.

Toto není nějaký formální problém, se kterými se matematici rádi vyřádí, existují dokonce i docela jednoduché integrály, u kterých se toto objeví, a obecně postup pro řešení takovýchto komplikací není nejjednodušší, jednu takovou situaci ukážeme v tomto příkladě v části Řešené příklad - Integrály. Často ale máme štěstí a výsledek vyjde rozumně, takže se vyplatí prostě se podívat, na jak velké množině jsou jak zadaná funkce, tak výsledek spojité, a tam by měl integrál fungovat.

3. Zbývají kombinace sinů a kosinů, které se nedají řešit předchozími dvěma triky. V tom případě nezbývá, než použít univerzální substituce. Tato substituce vlastně mohla být použita u všech příkladů v "goniometrickém šuplíku", ale jak hned uvidíme, rozhodně to není substituce, kterou by člověk dělal s radostí, jen se podívejte na transformační rovnice:

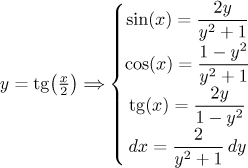
Odvození je zde. Jak je vidět, není problémem vyjádřit pomocí mocnin y všechny goniometrické funkce. Příklad:

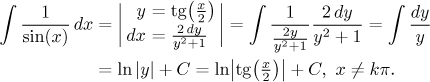
Tohle vlastně bylo docela snadné (i když ukázat, že se tento výsledek rovná vzorečku uvedenému na začátku je dost těžké). Bohužel, většinou to dopadne hůře. Zkusíme si třeba ukázat, jak by po univerzální substituci vypadal příklad, který jsme původně dělali substitucí y = tg(x):

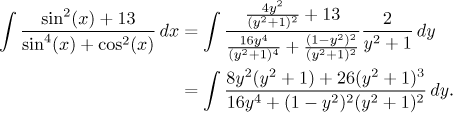
Teoreticky by to mělo jít umlátit parciálními zlomky, nicméně všimněte si, že ve jmenovateli bude polynom osmého stupně, takže je silně pochybné, jestli by se nám ho podařilo rozložit. Jak je vidět, tato univerzální substituce vede často k racionálním lomeným funkcím vysokých stupňů, proto je dobré znát ony triky uvedené výše, aby se jí člověk dokázal vyhnout, pokud to jde.

Teď zkusíme tyto postupy aplikovat na integrál z tan²(x). Coby mocnina by to mělo jít příslušným redukčním vzorcem:

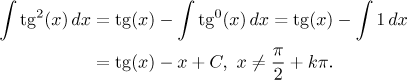
Pokud si vyjádříme tangens pomocí sinu a kosinu a umocníme, dostaneme rozumnou funkci se sudými mocninami sinu a kosinu. Znamená to, že tam není nic extra, co by umožnilo snadnou substituci, nicméně pořád se ještě dokážeme vyhnout té univerzální. Můžeme totiž použít tangensovou:

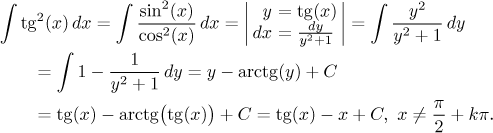
Zkušený integrátor by to ale stejně dělal ještě jinak:

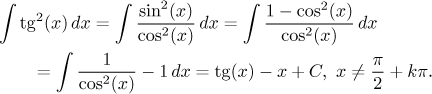
Prostě znát identity je nejlepší rada.

Další příklady goniometrických integrálů jsou k dispozici v části Řešené příklady - Integrace, jmenovitě zde, zde a zde.

Při výkladu posledních substitucí (sinové, tangensové a univerzální) jsme se omezili na trochu jednodušší případy, jmenovitě na racionální lomenou funkci R. Nebyl to takový problém, protože takto tyto substituce používáme nejčastěji, ale dají se také použít i v obecnějších případech, což je vyloženo v této poznámce. Může se to hodit.

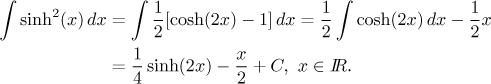
V části Řešené příklady - Integrace vede jedno řešení tohoto příkladu k hyperbolickému integrálu, který je tam řešen pomocí identit. Příklady vedoucí k integraci hyperbolických funkcí jsou i na konci části Přehled metod - Integrace - odmocnina z kvadrátu.

Na rozdíl od goniometrických funkcí máme ovšem ještě jednu alternativu: je možné za hyperbolické funkce dosadit z definice a při troše štěstí půjde výsledný výraz s exponenciálami integrovat. Tento přístup má jednu nevýhodu: Výsledek bude nějaká kombinace exponenciál, kterou bychom vzhledem k formě zadání měli zase převést na hyperbolické funkce; to je většinou dost velký problém. Někdy to ale není nutné (např. u určitých integrálů), pak je tento trik často velice efektivní.

Další šuplík: integrály s odmocninami z kvadrátů
Zpět na Přehled metod - Metody integrace