Příklad: Vypočítejte integrál
![]()
Řešení:
Při pohledu na integrál obvykle nejprve přemýšlíme o substituce. Zde se
nabízí myšlenka zjednodušit složenou funkci substitucí, klasicky si vezmeme
jako y vnitřní funkci x2. Na její úspěch pak
potřebujeme v integrálu najít
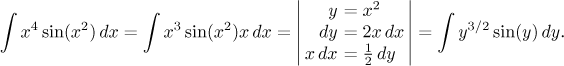
Tohle by vypadalo jako perfektní integrál pro per partes, jmenovitě typ "odstraňujeme mocniny", kdyby nebylo malého detailu: Mocnina u y není celočíselná. Proto ji nedokážeme vyrušit derivováním a integrace per partes selhává. Žádné jiné rozumné řešení se nenabízí, takže tato substituce sice fungovala, ale vedla na integrál, který neumíme našimi nástroji vyřešit.
Musíme se tedy poohlédnout po alternativách. Integrál nezapadá do žádného tematického šuplíku, ze základních metod jsme už vyřadili substituci, parciální zlomky jsou evidentně mimo a zbývá integrace per partes.
To dokonce vypadá jako přirozená volba. Integrand je už napsán jako součin dvou částí, z nichž jedna je mocnina x, které se snadno zbavíme opakovaným derivováním. problém ale nastane s druhým požadavkem, ýe by ta druhá část měla být snadno integrovatelná. Tak schválně: Zvolíme si následující přirozené označení,
![]()
Lehce teď najdeme
![]()
a na tento integrál nezabere žádná z metod, které zatím známe. Proč tomu tak
je? Jediná rozumná substituce by byla
Zkusíme tedy prohodit funkce:
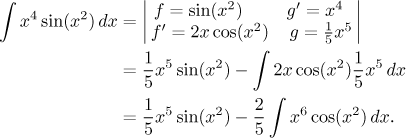
Teď jsme sice dokázali spočítat potřebné funkce a metodu per partes použít, ale ten poslední integrál je ještě horší než ten, se kterým jsme začali.
Co je tedy tím správným postupem? Klíčem k úspěchu je náš úplně první pokus. Když jsme zkusili přirozené přiřazení pro integrování per partes, tak jsme měli problém se získáním g. Už jsme ale viděli, že integrování funguje, když je tam jedno x navíc.
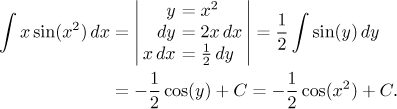
To x navíc se snadno zařídí, prostě si jedno x přesuneme z
f do
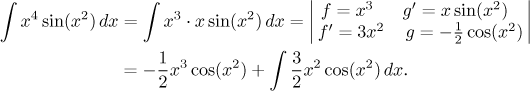
Ano, tak to má být, integrál zůstal v zásadě stejný, ale mocnina u x se snížila. Takže ještě jednou.
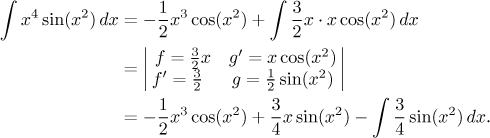
Skončili jsme s integrálem, který jsme před chvíli vzdali. Vzhledem k tomu,
že to byla naše poslední šance, je načase se zeptat, jestli jsme si jisti,
že na to naše metody nezaberou. Bohužel, odpověď zní, že ano. A nejen naše
metody, je známo, že integrál z
Protože každé integrování per partes snižeuje mocninu o dva, vidíme, že když
integrujeme
Takže to byly klasické metody. Co na to metody neklasické? Existuje způsob, a to pomocí mocninných řad. Rozvineme sinus a zbytek je snadný (pokud umíte zacházet s nekonečnými řadami).
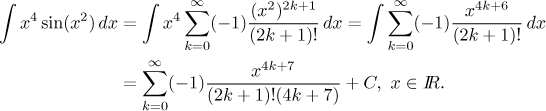
Tento výsledek není zrovna něco, co bychom běžně akceptovali jako odpověď, ale jsou aplikace, kde je takováto odpověď lepší než žádná.