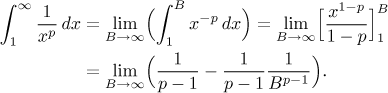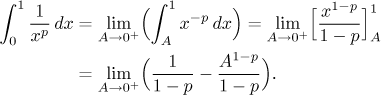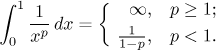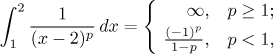Vlastnosti a příklady nevlastních integrálů

Protože nevlastní integrály jsou definovány limitou, většina vlastností určitého (Riemannova) integrálu stále platí. Například máme

Fakt.
(i) Pro všechny funkce f,g a reálná čísla k máme

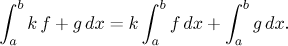
(ii) Pro všechny funkce f a reálná čísla a < b < c máme

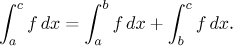
Každá z těchto rovností je chápána následujícím způsobem: Pokud integrál(y) na jedné straně rovnice konvergují, pak také konvergují výrazy na druhé straně a obě strany rovnice se rovnají.

(iii) Předpokládejme, že f a g jsou funkce jejichž integrály od a do b konvergují. Jestliže f ≤ g na (a,b), pak

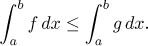
Třetí vlastnost je základem pro test konvergence založený na srovnání. Vysvětlíme jej v následující části, nicméně již teď vidíme, že by mělo být možné nějak funkce srovnat podle toho, jako dobře jejich integrály konvergují. Tomuto tématu se teď budeme věnovat. Víme, že pro kladné funkce jsou možné v zásadě jen dva druhy problémů, integrály v nekonečnu a svislé asymptoty. Začneme s tím prvním.

Mocniny v nekonečnu.

V předchozí části (Úvod do nevlastního integrálu) jsme ukázali, že

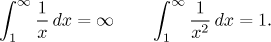
Škála mocnin je asi tou nejdůležitější a podíváme se na ně obecně. Protože víme, že abychom měli vůbec nějakou šanci na konvergenci, integrovaná funkce musí konvergovat k nule, je přirozené uvažovat mocniny v následujícím tvaru:

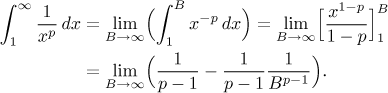
Limita konverguje tehdy a jen tehdy, když p > 1. Podotkněme, že tento výpočet byl chybný v případě, že p = 1, pak totiž integrace dává logaritmus, ale tento příklad jsme již spočítali dříve a dostali divergentní integrál. Formálně tedy dostaneme

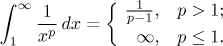
Tento obrázek by měl pomoci:

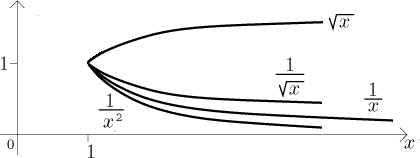
Obsah po grafem 1/x je nekonečný. Pokud dáme do jmenovatele menší mocninu, pak se graf zvedne a obsah pod ním bude přirozeně zase nekonečný. Pokud naopak mocninu ve jmenovateli zvýšíme, funkce klesne a předchozí výpočet ukazuje, že obsah pod grafem je teď konečný. Jinými slovy, funkce 1/x je přesně tím momentem, kdy se divergence mění na konvergenci, přičemž funkce samotná dává divergentní integrál.

Tohle je asi ten správný moment k poukázání na podstatný rozdíl v terminologii a významu. Ačkoliv funkce 1/x samotná je v nekonečnu konvergentní (jmenovitě konverguje k nule), její integrál do nekonečna (například od jedné jako nahoře) je divergentní.

Všimněte si také další důležité věci. Konvergence či divergence těchto mocninných integrálů není ovlivněna volbou dolní meze (pokud je tedy větší než nula). To je zcela přirozené, protože tyto funkce mají problémy jen v nekonečnu a v nule. Pokud odejmeme konečnou část z oblasti o nekonečném obsahu, zbylá část má pořád nekonečný obsah. Podobně nemůžeme "zkazit" oblast o konečném obsahu tím, že bychom přidali/odebrali konečnou oblast. Toto vlastně vyplývá z vlastnosti (ii) nahoře. Samozřejmě, pokud se například v předchozím příkladě rozhodneme integrovat od 2 do nekonečna, ty konvergentní mocniny dají odlišný výsledek (ale nemohou dát nekonečno).

Mocniny v nule.

Opět se podíváme na nejjednodušší případ a předpokládáme, že p ≠ 1:

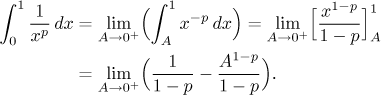
Tentokráte limita konverguje přesně v případě, že p < 1. Snadný výpočet s logaritmem coby primitivní funkcí ukazuje, že i integrál s p = 1 je divergentní, takže dostaneme

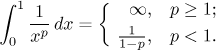
Máme proto následující obrázek:

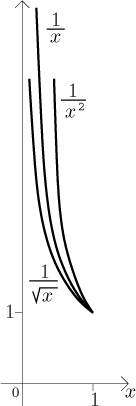
Funkce 1/x (s divergentním obsahem pod sebou) je zase dělící hranicí mezi konvergencí a divergencí. Všimněte si, že tyto mocniny vlastně fungují jako "vahadla". Začneme s grafem 1/x, pod kterým jsou nekonečné obsahy "na obou koncích", u 0 a u nekonečna. Pokud zvýšíme mocninu, pravý konec klesne (konvergentní integrál) a levý se zvedne (divergentní integrál). Pokud mocninu snížíme, situace se obrátí.

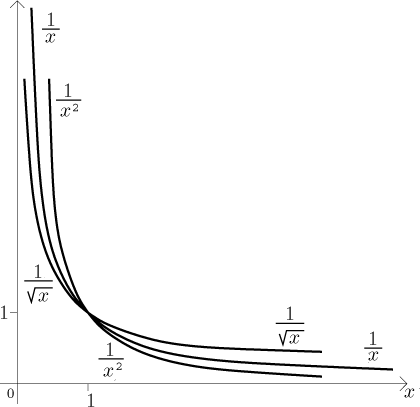
Existují funkce, které vypadají velice podobně, ale mají konvergentní integrály u 0 a také u nekonečna; jinými slovy, pokud je integrujeme od 0 do nekonečna (přičemž daný integrál musíme rozdělit na dva integrály, každý s jedním problémem), dostaneme konvergentní výsledek. Právě provedené výpočty ukazují, že obyčejná mocnina by tohle nedokázala, musí se zkusit něco komplikovanějšího.

Problémy v jiných bodech se zkoumají podobně. Situace v mínus nekonečnu je vlastně stejná jako v nekonečnu (s tím rozdílem, že ne všechny mocniny jsou na záporné poloose definovány). Také chování v nule zleva je stejné jako v nule zprava, zase je tady problém s existencí některých mocnin. Svislé asymptoty v jiných bodech jsou prostě jen posuny svislé asymptoty v nule, takže například:

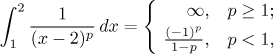
což ale platí pouze pro p, pro které je mocnina definovaná na (1,2), například p = 1/3 funguje, ale pro p = 1/2 problém nemá smysl.

Testy konvergence
Zpět na Teorie - Nevlastní integrály