Věta (Srovnávací kritérium, srovnávací test).
Nechť b je reálné číslo nebo
Jestliže 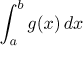 konverguje,
pak také
konverguje,
pak také 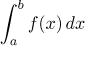 konverguje.
konverguje.
Jestliže 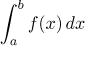 diverguje,
pak také
diverguje,
pak také 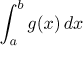 diverguje.
diverguje.
Často nás vlastně nezajímá přesná hodnota integrálu, jen potřebujeme vědět, jestli konverguje. Protože většina integrálů se počítá těžce, obvykle je jednodušší porovnat integrovanou funkci s jinou jednodušší funkcí a na základě tohoto srovnání vyvodit nějaký závěr. V této části se budeme zabývat jen základními nevlastními integrály - tedy s jedním "problémem". Obecnější integrály se vždy řeší rozdělením na více integrálů základního typu, testy konvergence pak mohou být aplikovány na každý zvlášť. Protože situace je symetrická, podíváme se na testy konvergence pro situaci, kdy je problém v pravém koncovém bodě. Abychom si ulehčili starosti s integrovatelností, budeme pracovat se spojitými funkcemi; věty jsou ovšem pravdivé i obecněji.
Nejprve budeme předpokládat, že se funkce, které uvažujeme, jsou kladné. To silně zjednoduší situaci. Jak už jsme viděli předtím, v takovém případě jsou pouze dvě alterativy: Buď má oblast pod grafem obsah konečný, nebo nekonečný.
Věta (Srovnávací kritérium, srovnávací test).
Nechť b je reálné číslo nebob = ∞, nechťa < b. Nechť f a g jsou funkce spojité a nezáporné na⟨a,b) af ≤ g na⟨a,b). Jestliže
konverguje, pak také
konverguje.
Jestliže
diverguje, pak také
diverguje.
Myšlenka tohoto kritéria by měla být jasná z obrázku:
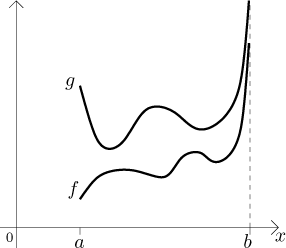
Jestliže je pod grafem g konečný obsah, tak menší oblast pod grafem f musí mít také konečný obsah. Pokud je naopak pod grafem f nekonečný obsah, pak větší oblast pod grafem g musí mít také nekonečný obsah.
Z obrázku je také zjevné, že srovnání funguje jen jedním směrem a že citované dvě implikace nemohou být pravdivé jako ekvivalence. Předpokládejme například, že oblast pod grafem f má konečný obsah. Protože oblast pod grafem g je větší, není možné udělat žádný závěr: její obsah může být konečný i nekonečný. Toto je hlavní nevýhoda Srovnávacího kritéria.
Příklad: Rozhodněte, zda tento integrál konverguje:
![]()
Tento integrál jde vlastně spočítat pomocí parciálních zlomků, ale bude
jednodušší odpovědět pomocí srovnávacího kritéria. Všimneme si, že pro kladné
x je
![]() .
Protože integrál
.
Protože integrál
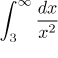 konverguje (to si pamatujeme, viz
Vlastnosti a příklady), podle
srovnávacího kritéria konverguje i daný integrál.
konverguje (to si pamatujeme, viz
Vlastnosti a příklady), podle
srovnávacího kritéria konverguje i daný integrál.
Právě jsme viděli hlavní výhodu srovnávacího testu: velmi často je velmi snadný. Tento příklad byl typický. Je-li dána (komplikovaná) funkce, najdeme testovací funkci, typicky mocninu, protože jejich chování dobře známe. Pak se pokusíme dokázat nějakou nerovnost. Pokud máme štěstí, dostaneme docela snadno závěr. Pokud štěstí nemáme, potkáme v praxi hlavní nevýhodu srovnávacího kritéria:
Příklad: Rozhodněte, zda tento integrál konverguje:
![]()
I tento integrál by šlo vypočítat přes parciální zlomky, ale zkusíme
srovnávací kritérium. Všimneme si, že pro kladné x je
![]() .
Testovací integrál
.
Testovací integrál
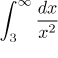 konverguje (jako předtím), ale tentokráte jde srovnávací nerovnost špatným
směrem a žádný závěr není možný. Srovnávací test (tak jak byl použit) selhal.
Je nutno přiznat, že tento problém by ve skutečnosti šlo vyřešit pomocí
srovnávacího kritéria, ale vyžaduje to pečlivější volbu testovací funkce
g. Důkaz vzniklé nerovnosti vyžaduje určitou práci, takže nakonec je
jednodušší prostě použít jiný test. Zvědavý čtenář najde řešení přes
srovnávací kritérium
zde.
konverguje (jako předtím), ale tentokráte jde srovnávací nerovnost špatným
směrem a žádný závěr není možný. Srovnávací test (tak jak byl použit) selhal.
Je nutno přiznat, že tento problém by ve skutečnosti šlo vyřešit pomocí
srovnávacího kritéria, ale vyžaduje to pečlivější volbu testovací funkce
g. Důkaz vzniklé nerovnosti vyžaduje určitou práci, takže nakonec je
jednodušší prostě použít jiný test. Zvědavý čtenář najde řešení přes
srovnávací kritérium
zde.
Tento příklad ukázal, že nestačí najít jen nějaké srovnání. Je-li dána funkce f, zkoušíme najít vhodnou (jednoduchou) testovací funkci. Pokud existuje přirozený kandidát h, který je menší než f, pomůže pouze v případě, že jeho integrál diverguje; takové h bychom tedy hledali, pokud bychom podezřívali f z divergentního integrálu a chtěli to dokázat. Pokud existuje přirozený kandidát g, který je větší než f, bude užitečný jen v případě, že jeho integrál konverguje; takovou testovací funkci bychom se snažili najít v případě, kdy si myslíme, že integrál z f konverguje.
Srovnávací kritérium může být považován za zobecnění následujícího faktu (viz Vlastnosti Riemannova integrálu):
Jestliže f a g jsou Riemannovsky integrovatelné na
⟨a,b⟩ af ≤ g na⟨a,b⟩, pak
Srovnávací kritérium v zásadě říká, že totéž platí i pro nezáporné funkce a
nevlastní integrály. Pak už ovšem nejde striktně o nerovnost, spíše to má
následující smysl: Pokud je ten "menší" integrál nekonečný, pak ten
"větší"
musí být přirozeně také nekonečný, protože jen nekonečno splňuje nerovnost
Pokud je naopak ten "větší" integrál konečný, pak by měl být konečný i ten "menší" a musí mít hodotu menší nebo rovnou. Tento "přístup přes nerovnost" také pěkně ukazuje, proč srovnávací kritérium funguje jen jedním směrem. Ukážeme to tím, že se vrátíme k prvním dvěma příkladům.
V prvním příkladě si můžeme představit, že integrováním nerovnosti
![]() dostaneme
nerovnost
dostaneme
nerovnost
![]()
Teď se zdá přirozené, že daný integrál by měl být také konvergentní, dokonce dostaneme horní odhad pro jeho hodnotu.
V druhém příkladě si můžeme představit, že integrováním nerovnosti
![]() dostaneme
nerovnost
dostaneme
nerovnost
![]()
V této nerovnosti může být daný integrál roven konečnému číslu, ale také
nekonečnu (protože určitě
Teď už by také mělo být jasné, proč požadujeme, aby byla funkce f nezáporná. Kdybychom jí dovolili spadnout pod osu x, neměli bychom žádnou kontrolu nad tím, kolik obsahu si tam nabere. Srovnávací kritérium pro funkci, která hodně mění znaménko, by tedy musel obsahovat dvě testovací funkce, jedna by zabránila, aby f bylo moc velké, a druhá by mu bránila nabrat příliš mnoho obsahu pod osou x. Obvykle ovšem není takto komplikovaný test nutný a vystačíme si s jednodušším (ale méně silným) testem, srovnávacím kritériem, které si hlídá f pomocí absolutní hodnoty:
Věta (Srovnávací kritérium - verze s absolutní hodnotou).
Nechť b je reálné číslo nebob = ∞, nechťa < b. Nechť f a g jsou funkce spojité na⟨a,b) a nechť| f | ≤ g na ⟨a,b). Jestliže
konverguje, pak také
konverguje.
Následující test je mnohem silnější nástroj než srovnávací kritérium. Například jeho závěr je ve tvaru ekvivalence, takže nesdílí hlavní nevýhodu srovnávacího kritéria. Jeho hlavní nevýhodou je, že jeho správné použití vyžaduje více práce.
Věta (Limitní srovnávací kritérium, limitní srovnávací test).
Nechť b je reálné číslo nebob = ∞, nechť a < b. Nechť f a g jsou funkce spojité na⟨a,b), nechť tam platíf ≥ 0. Předpokládejme, že limitaexistuje konečná, ale není rovna nule. Pak integrál
konverguje tehdy a jen tehdy pokud konverguje integrál
.
Tento test funguje trochu jinak. Je-li dána funkce f, hledáme
testovací funkci g, která nemusí být nutně menší či větší než
f; klidně může kolísat a být chvíli nad a chvíli pod f.
Důležité je, že když se x blíží k b (ze správné strany, tj. od
a), tak se tyto dvě funkce víceméně rovnají (až na násobek). To se
ověří právě tou limitou v Limitním srovnávacím kritériu. Dokážeme tím, že je
naše odhadnutá testovací funkce správně zvolena. V typickém případě (pro
"správný" odhad testovací funkce) ta limita vyjde rovna jedné.
Matematicky to znamená, že když x se blíží k b, je podíl
![]() zhruba jedna.
Roznásobením získáme, že když je x blízko k b, pak
zhruba jedna.
Roznásobením získáme, že když je x blízko k b, pak
![]()
Takže tyto integrály by měly vyjít zhruba stejně, závěr věty pak následuje. Je-li jeden integrál konečný, musí být i ten druhý. Jestli jeden diverguje, tak i ten druhý.
Limitní srovnávací kritérium platí i pro funkce, které jsou vždy záporné. Dokonce platí i pro funkce, které nedrží všude stejné znaménko. Aby ale fungovalo, změna znaménka se nesmí přihodit "příliš často". Protože přesná specifikace stojí víc práce, než přináší užitku, většinou se tyhle obecnosti ignorují a pracuje se jen s citovaným testem pro nezáporné funkce.
Příklad: Rozhodněte, zda tento integrál konverguje:
![]()
Když je x blízko k nekonečnu, tj. když je to opravdu velké číslo, tak
ve jmenovateli převáží druhá mocnina a můžeme ten zbytek ignorovat. To
motivuje naší volbu testovací funkce:
![]()
Limita existuje a není rovna nule, takže daná funkce a testovací funkce jsou
opravdu velmi podobné blízko nekonečna. Protože víme, že integrál
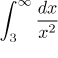 konverguje, vyplývá z toho, že i daný integrál konverguje.
konverguje, vyplývá z toho, že i daný integrál konverguje.
Toto bylo typické použití Limitního srovnávacího kritéria. Nejprve jsme našli testovací funkci, pak jsme použili limitu k důkazu, že to byla správná volba. Potom jsme prozkoumali konvergenci testovacího integrálu a obdržený výsledek platil i pro daný integrál. Pro shrnutí strategie pro výběr správné testovací funkce a příklady odkazujeme na Přehled metod - Nevlastní integrály a Řešené příklady - Nevlastní integrály.
Je třeba poznamenat, že Limitní srovnávací kritérium není lepší (ve smyslu obecnější) než Srovnávací kritérium. Existují problémy, kde je možné najít srovnání přes nerovnost, zatímco limitní srovnání je v zásadě nemožné. Jeden takový problém je v části Řešené příklady - Nevlastní integrály.
Všechny tři výše uvedené testy mají verze, které se věnují problému v levém koncovém bodě integračního intervalu. Protože jde o evidentní modifikace, raději jen ukážeme na jednom příkladě, jak to funguje. Využijeme také této příležitosti k tomu, abychom ukázali, jak se pracuje s případem svislé asymptoty.
Příklad: Rozhodněte, zda tento integrál konverguje:
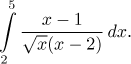
Máme problém v bodě ![]() . Toto
tvrzení musí být ověřeno:
. Toto
tvrzení musí být ověřeno:
![]()
Vidíme, že náš odhad byl správný, protože limita dala nenulové číslo. Teď se musíme podívat na odpovídající nevlastní integrál testovací funkce:
![]()
Tento integrál diverguje, protože je to jedna z mocnin, které jsme probírali v části Vlastnosti a příklady a pamatujeme si to. Podle Limitního srovnávacího kritéria diverguje i daný integrál.
Toto řešení přesně následovalo Limitní srovnávací kritérium, ale možná by stálo za
to se blíže podívat na smysl toho, co se dělalo. Limitní výsledek v našem
srovnání znamená, že pokud je x opravdu blízko k 2 (zprava), tak
![]() .
To pak implikuje podobnost mezi jejich integrály od 2 doprava. Odmocnina ze
dvou je multiplikativní konstanta, takže je ji možné vytknout z integrálu a
dostaneme srovnání
.
To pak implikuje podobnost mezi jejich integrály od 2 doprava. Odmocnina ze
dvou je multiplikativní konstanta, takže je ji možné vytknout z integrálu a
dostaneme srovnání
![]() .
Protože testovací integrál napravo diverguje a vynásobení nenulovým číslem to
nemůže napravit, musí divergovat i ten integrál nalevo. Vidíme zároveň, že
multiplikativní konstantu, která nám vyjde při limitním srovnání, můžeme
během úvah ignorovat, protože neovlivní konvergenci integrálů (na to ale musí
být nenulová).
.
Protože testovací integrál napravo diverguje a vynásobení nenulovým číslem to
nemůže napravit, musí divergovat i ten integrál nalevo. Vidíme zároveň, že
multiplikativní konstantu, která nám vyjde při limitním srovnání, můžeme
během úvah ignorovat, protože neovlivní konvergenci integrálů (na to ale musí
být nenulová).
Čtenáři teď možná vrtá hlavou, jak jsme přišli na tu testovací funkci. To je správná otázka, protože to může být občas docela těžké a hlavně to vyžaduje dost zkušeností. Proto se také většinou Limitní srovnávací kritérium aplikuje na problémy s nekonečnem, popř. mínus nekonečnem. Tam si prostě představíme, že x je hodně velké číslo, a intuice nám již napoví, které části dané funkce se stanou nedůležité.