Průměr funkce

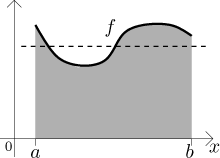
Nechť f je funkce na intervalu ⟨a,b⟩. Chceme spočítat její průměr. Umíme najít průměr konečného počtu čísel - sečteme je a vydělíme jejich počtem. Teď se pokusíme aplikovat tuto myšlenku na funkci na intervalu.

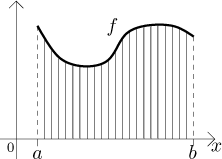
Rozdělme interval ⟨a,b⟩ na disjunktní podintervaly velikosti dx (viz zde pro vysvětlení dx) a pak rozdělme oblast pod grafem f na odpovídající svislé pruhy.

Protože tyto podintervaly jsou tak malé, změnu f uvnitř každého z nich můžeme ignorovat. Průměr f lze tedy zjistit spočítáním průměru výšek všech pruhů. Kolik těchto pruhů máme? To je jednoduché, každý pruh má šířku dx a dohromady musí dát velikost intervalu ⟨a,b⟩. Průměr f by tedy měl být

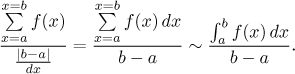
Tato úvaha vede k následující definici průměru dané funkce, zvaného také střední hodnota:

Definice.
Nechť f je Riemannovsky integrovatelná funkce na ⟨a,b⟩. Definujeme průměr f na tomto intervalu vzorcem

Všimněte si, že dostáváme

Toto je zajímavé ze dvou důvodů. Za prvé, podle Věty o střední hodnotě pro integrály, pokud je f spojitá, pak musí nabývat svého průměru v nějakém bodě z ⟨a,b⟩. Všimněte si, že spojitost je naprosto nutná. Stačí si vzpomenout na příklad skokové funkce. Její průměr na ⟨0,2⟩ je 3/2, ale tato funkce není nikdy rovna 3/2.

Zmíněná rovnost je také zajímavá z geometrického pohledu. Říká totiž následující: Pokud se podíváme na oblast pod grafem f a zarovnáme její horní stranu na úrovni průměru f, výsledný obdélník má stejný obsah jako ta oblast pod grafem f.

Obsah
Zpět na Teorie - Aplikace