Věta.
Nechť f je Riemannovsky integrovatelná funkce na
![]()
a
![]()
Zde se podíváme na některé vlastnosti Riemannova integrálu, které nejsou přímo svázány s jeho výpočtem, ale jsou spíše teoretické povahy.
Věta.
Nechť f je Riemannovsky integrovatelná funkce na⟨a,b⟩. Pak platí
a
Všimněte si, že integrály v limitách mají smysl. Podívejme se na první
rovnost: Předpokládáme, že f je Riemannovsky integrovatelná na
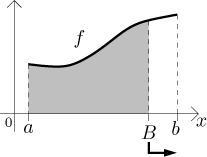
Pokud odřízneme kousek oblasti podél pravé hrany a odřezávanou část zmenšujeme, výsledné obsahy by měly konvergovat k celému obsahu.
Podobně je f Riemannovsky integrovatelná na
Druhá vlastnost, kterou zde probereme, je modifikace standardní Věty o střední hodnotě (viz Derivace - Teorie - Věta o střední hodnotě) pro funkci F definovanou v části Základní věta integrálního počtu:
![]()
Fundamentální věta pak říká
![]()
Když dosadíme za F, dostáváme následující větu.
Věta (Věta o střední hodnotě pro integrály, Lagrangeova věta pro integrály).
Nechť f je spojitá funkce na⟨a,b⟩. Pak existuje číslo c z intervalu(a,b), pro které platí
Pokud si vzpomeneme na definici průměru funkce f (viz Aplikace - Průměr), Větu o střední hodnotě můžeme zapsat takto:
Věta.
Nechť f je spojitá funkce na⟨a,b⟩. Pak existuje číslo c z(a,b) takové, žef (c) se rovná průměru funkce f na intervalu⟨a,b⟩.
Spojitost předpokládaná ve větě je nutná. Stačí si vzpomenout na příklad
skokové funkce. Její průměr
na
Věta o střední hodnotě pro integrály má mnoho verzí. Ta uvedená výše je asi nejpopulárnější, ale také nejslabší, je to jen reformulace staré dobré Lagrangeovy věty. Existují mnohem silnější tvrzení, ukážeme zde jedno z populárnějších.
Věta (Věta o střední hodnotě pro integrály).
Nechť je f spojitá funkce na[a,b] a g je integrovatelná funkce na[a,b], která je tam kladná. Pak existuje číslo c z(a,b) takové, že
Všimněte si, že když tuto větu použijete s konstantní funkcí