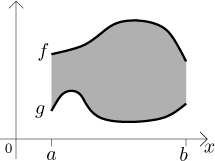
Uvažujme oblast vymezenou shora grafem funkce f a zdola grafem funkce
g na intervalu

Pokud jsou obě funkce Riemannovsky integrovatelné, obsah této oblasti je roven
![]()
Příklad: Najděte obsah oblasti vymezené funkcemi
Řešení: Nejprve nakreslíme obrázek:
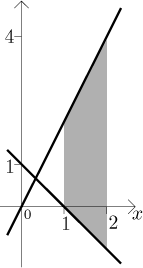
Vidíme, že
![]()
Pokud potřebujeme najít obsah komplikovanější oblasti, musíme ji rozložit na oblasti základního typu a pak sečíst jednotlivé obsahy. To je například nutné v případě, že se zadané funkce proplétají - někdy je větší jedna, jindy druhá.
Někdy ušetří spoustu času jeden dobrý trik: prohození os. Obrázek se otočí podle hlavní diagonály, funkce se promění ve své inverzní funkce a integrál používá dy.
Příklad: Najděte obsah oblasti pod grafem funkce
Řešení: Nejprve namalujeme obrázek:
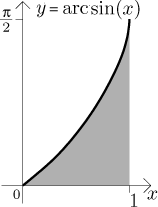
Obsah je
![]()
Tento integrál se počítá pomocí integrace per partes, což vlastně není tak hrozné, ale čas to zabere. Příklad se stane snažším, pokud prohodíme osy:
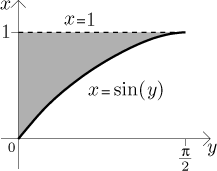
Obsah teď lehce najdeme:
![]()
Pokud vás zajímá, jak intuitivně sestavit správný integrál a jak se rozhodnout, zda prohodit osy či ne, podívejte se na druhý řešený příklad. Ukážeme tam, že k nalezení obsahu jsou vlastně dva přístupy. Jeden je si pamatovat uvedený vzorec a aplikovat jej, což může být občas trochu matoucí u složitějších příkladů. Druhý přístup je si pamatovat hlavní myšlenku za tímto vzorcem, tj. ten trik s proužky, a aplikovat jej na daný příklad.
Uvažujme parametrickou křivku
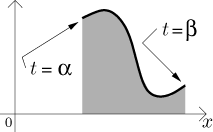
Jestliže
![]()
Uvažujme křivku danou v polárních souřadnicích předpisem
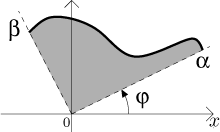
Jestliže
![]()