Absolutní konvergence

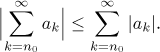
Definice.
Uvažujte řadu  ∑ a_k. Řekneme, že konverguje absolutně, nebo že je absolutně konvergentní, pokud řada  ∑ |a_k|  konverguje.

Jaký je vztah mezi touto definicí a obvyklou konvergencí? Za prvé, vidíme, že když máme řadu, jejíž členy jsou všechny kladné (nebo nulové), pak absolutní hodnota neznamená žádný rozdíl. Pro takové řady se proto pojem absolutní konvergence shoduje s pojmem konvergence. Pro obecné řady je to ovšem něco jiného. Jestliže má řada nějaké záporné členy, tak absolutní hodnota změní tyto mínusy v plusy a dostaneme jinou řadu. Má její konvergence nějaký vztah ke konvergenci řady původní, popřípadě naopak?

Věta.
Jestliže řada  ∑ a_k  konverguje absolutně, pak nutně konverguje.
Navíc pak máme odhad

Tato nerovnost je vlastně zobecněním klasické "trojúhelníkové nerovnosti" |x + y| ≤ |x| + |y| na nekonečně mnoho sčítanců.

Vidíme, že pojem absolutní konvergence je silnější než obvyklá konvergence; je to "lepší konvergence". Tvrzení lze také obrátit. Jestliže je řada divergentní, pak nemůže být absolutně konvergentní. Implikace v opačných směrech ale obecně neplatí. Jinými slovy, pokud zjistíme, že absolutní konvergence pro nějakou řadu selže, tak to nepomůže při zkoumání její konvergence. Nebo jinak, konvergentní řada může a nemusí být absolutně konvergentní (viz příklad níže).

Máme tedy následující obrázek. Představte si množinu všech možných řad. Některé z nich jsou "lepší", jsou konvergentní. Mezi nimi jsou některé ještě "lepší", ty jsou absolutně konvergentní. Ty uprostřed, konvergentní ale ne absolutně konvergentní, si zaslouží jméno.

V české literatuře se používá název "neabsolutní", takže se ho tu budeme držet, ale nedělám to rád, sám dávám přednost alternativě "podmínečná", protože mi přijde mnohem výstižnější. Slovo "podmínečně" naznačuje, že taková řada konverguje, ale jen tak tak a snadno se to zkazí. Absolutní konvergence je mnohem robustnější, dost toho přežije. Pro několik tvrzení, která tyto pocity ospravedlňují, se podívejte na Věty níže.

Příklady:
1. Řada     je divergentní.
Tím je vše řečeno, mimo jiné nemůže být absolutně konvergentní.

2. Řada     je konvergentní (viz Příklad na Leibnizovo kritérium v části Teorie - Testování konvergence - Konvergence obecných řad), ale když aplikujeme absolutní hodnotu na jednotlivé členy, dostaneme harmonickou řadu, o které víme, že diverguje.
Proto     není absolutně konvergentní, ale konverguje neabsolutně.

3. Řada     je konvergentní (to se snadno dokáže pomocí Leibnizova kritéria). Je také absolutně konvergentní? Pokud aplikujeme absolutní hodnotu na všechny členy, dostaneme řadu   , o které víme, že také konverguje, viz příslušný příklad v části Teorie - Důležité příklady.
Proto řada     konverguje absolutně.

Začneme následujícími užitečnými fakty.

Fakt.
(i) Skalární násobek každé absolutně konvergentní řady zase konverguje absolutně.
(ii) Součet dvou absolutně konvergentních řad také konverguje absolutně.
(iii) Jestliže alespoň jedna ze dvou daných konvergentních řad konvegruje absolutně, pak jejich Cauchyho součin také konverguje.
(iv) Cauchyho součin dvou absolutně konvergentních řad také konverguje absolutně.

Už jsme naznačili, že absolutní konvergence je podstatně lepší než obyčejná konvergence (tj. neabsolutní konvergence). Ukážeme tři věty, které tento názor podpírají.

Věta.
Předpokládejme, že  ∑ a_k  je konvergentní řada.
(i) Jestliže konverguje absolutně, pak také řada  ∑ ε_ka_k  konverguje pro libovolnou volbu znamének ε_k = ±1.
(ii) Jestliže konverguje neabsolutně, pak existuje volba znamének ε_k = ±1 taková, že  ∑ ε_ka_k = ∞.

Tvrzení (ii) by nemělo být překvapením. Jestliže daná řada nekonverguje absolutně, tak změnou všech znamének na plus dostaneme řadu s nekonečným součtem. Následující tvrzení také nezní nějak překvapivě.

Věta.
Předpokládejme, že  ∑ a_k  je konvergentní řada.
(i) Jestliže konverguje absolutně, pak také každá její vybraná řada konverguje.
(ii) Jestliže konverguje neabsolutně, tak existuje její vybraná řada, která diverguje do nekonečna.

Například jsme už poznamenali, že když vezmeme všechny liché členy v alternující řadě výše (Příklad 2), tak dostaneme divergentní řadu.

To opravdu zajímavé jsme si nechali nakonec.

Věta.
Předpokládejme, že  ∑ a_k  je konvergentní řada.
(i) Jestliže konverguje absolutně, pak také každé její přerovnání konverguje a jeho součet je stejný jako součet původní řady.
(ii) Jestliže konverguje neabsolutně, pak pro každou konstantu c reálnou či plus/mínus nekonečno existuje přerovnání splňující  ∑ a_P(k) = c.

Musím přiznat, že když jsem tohle slyšel poprvé, padl jsem na zadek. Připomínáme, že přerovnání znamená, že si ponecháme všechny členy včetně jejich znamének, jen přerovnáme pořadí, ve kterém jsou sčítány. To znamená, že můžeme vzít například tuto báječnou řadu , o které víme, že je neabsolutně konvergentní, a jen změnou pořadí jejích sčítanců ji přinutíme, aby se nasčítala do nekonečna. A jiným přerovnáním naprosto stejných členů dostaneme mínus nekonečno. Nebo třeba 13 či libovolné jiné číslo, které si vyberete. Podivné, ale pravdivé. Toto neodvolatelně ukazuje, že sčítat nekonečně mnoho čísel je opravdu jiné než sčítat konečně mnoho čísel, třeba nelze očekávat obecný komutativní zákon. Tomu úžasnému tvrzení (ii) se také říká Riemannova věta.

Na druhou stranu vidíme, proč je absolutní konvergence tak populární: Dává nám spoustu volnosti, například se nemusíme bát přerovnat členy, řada pořád půjde ke stejnému číslu.

Poznámka: Existuje také pojem bezpodmínečné konvergence. Řekneme, že daná řada konverguje bezpodmínečně, jestliže všechna její přerovnání také konvergují. Dá se ukázat, že tento požadavek je ekvivalentní ještě jinému: Řada konverguje bezpodmínečně, pokud konverguje nezávisle na tom, jaká znaménka dáme před jednotlivé členy.

Věty nahoře ukazují, že pro reálnou řadu jsou tyto vlastnosti ekvivalentní absolutní konvergenci. Jsou také totožné pro řady komplexních čísel a vlastně pro řady v libovolném konečně dimenzionálním prostoru, ale liší se v nekonečně dimenzionálních prostorech, což je vysoce nad úrovní Math Tutoru a tak to budeme ignorovat. V "našem" světě jsou tyto pojmy ekvivalentní a s absolutní konvergencí se pracuje rozhodně lépe než s bezpodmínečnou, proto v zásadě nikdo tu druhou nepoužívá. Jak už jsem poznamenal výše, mi se líbí její doplněk, název "podmínečná konvergence", protože je výstižnější než "neabsolutní konvergence" a my už teď víme, že jsou to ekvivalentní pojmy.

Poznámka o komutativitě: Poslední věta říká, že si při práci s konvergentní řadou (když nevíme, zda konverguje absolutně nebo neabsolutně) nemůžeme dovolit přerovnat její členy. Na druhou stranu, u absolutně konvergentní řady to klidně můžeme udělat a ještě věci navíc. Co třeba tohle: Dostali jsme řadu a my ji rozdělíme na dvě vybrané řady, ty pak zase sečteme. Můžeme očekávat, že dostaneme tentýž výsledek? Věta nahoře říká, že ne obecně, protože ty vybrané řady, které vytvoříme, mohou divergovat. Na druhou stranu problém nebude, pokud víme, že daná řada konverguje absolutně, pak můžeme dokonce i změnit pořadí. Indukcí lze toto rozšířít i na více řad, dostaneme pak následující tvrzení.

Můžeme vzít součet několika absolutně konvergentních řad, vzít všechny členy všech řad, které se v něm vyskytují, sesypat je na hromádku, rozdělit do úplně nových řad a pak je sečíst - aniž bychom změnili výsledek.

Zpět na Teorie - Úvod do řad