Věta (odmocninové kritérium pro obecné řady).
Uvažujme řadu
![]()
konverguje.
• Jestliže
• Jestliže
Zatímco pro řady s nezápornými členy máme spoustu testů, většinu ztratíme v okamžiku, když dovolíme členům řady měnit znaménka. Je velice málo testů, které by fungovaly pro obecné řady. Těmi tedy začneme. Pak se podíváme na Leibnizovo kritérium, budeme diskutovat absolutní konvergenci a sekci uzavřeme s Abelovým kritériem a Dirichletovým kritériem.
Nejjednodušší obecný test je
Nutná podmínka konvergence.
Jestliže posloupnost {ak} nejde k nule, tak řada∑ ak diverguje.
(Viz Základní vlastnosti v části Teorie - Úvod.) Je to ale jen implikace a bohužel pomůže jen zřídka. Mnohem užitečnější (i když rozhodně ne univerzálně použitelné) jsou verze populárních odmocninového a podílového kritéria pro obecné řady.
Věta (odmocninové kritérium pro obecné řady).
Uvažujme řadu∑ ak. Předpokládejme, že limita
konverguje.
• Jestližeϱ < 1, pak daná řada konverguje.
• Jestližeϱ > 1, pak daná řada diverguje.
Věta (podílové kritérium pro obecné řady).
Uvažujme řadu∑ ak. Předpokládejme, že limita
konverguje.
• Jestližeλ < 1, pak daná řada konverguje.
• Jestližeλ > 1, pak daná řada diverguje.
(Viz poznámka na konci sekce Odmocninové a podílové kritérium v části Teorie - Testování konvergence.) Jako obvykle v případech, kdy tyto konstanty vyjdou rovny 1, nemůžeme říst o dané řadě nic.
Často se vyskytnou případy, kdy se znaménka v řadě střídají ...+ − + − +... (tedy řada je alternující) a členy jsou v absolutní hodnotě klesající. V takovém případě jde o nejlepší možnou situaci, protože máme jednoduchý test konvergence, který dává kompletní informaci.
Věta (Leibnizovo kritérium).
Uvažujme řadu, kterou lze vyjádřit jako∑ (−1)kbk pro nějaká kladná bk, která tvoří nerostoucí posloupnost.
Tato řada konverguje tehdy a jen tehdy, když posloupnost{bk} jde k 0.
Poznamenejme, že jeden směr ve větě je triviální. Pokud čísla
bk nejdou k nule, pak také členy řady
Všimněte si, že ten test také funguje na řady, jejichž znaménka jdou přesně
opačně, formálně
Příklad: Vyšetřete konvergenci řady
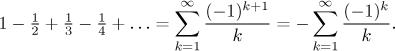
Vidíme, že každý člen dané řady lze vyjádřit jako
Poznamenejme, že také šlo změnit tuto řadu na "správnou alternující" následující změnou indexace:
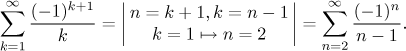
Pak můžeme použít Leibnizovo kritérium s
Několik ukázek lze najít v části Řešené příklady - Testování konvergence, jmenovitě tento příklad a tento příklad.
V pokročilejších kursech se studenti učí také méně populární testy, které mohou pomoci i s jinými kombinacemi znamének než je ta alternující situace. Na konci této sekce ukážeme Dirichletovo kritérium, které je možné vidět jako zobecnění Leibnizova kritéria na komplikovanější vzorce znamének.
Samozřejmě v situaci, kdy členy řady mění znaménka, bychom museli mít
opravdu štěstí, aby byla alternující, protože je mnoho způsobů, kterými se
znaménka mohou měnit. Pak nelze použít Leibnizovo kritérium, dokonce ani
když znaménka sledují určitý vzor (například dva plusy vždy následované
jedním mínusem a tak). Všimněte si mimochodem, že v situaci
Pokud zjistíme, že řada
Může se ovšem také stát, že řada s absolutními hodnotami diverguje, a pak o konvergenci dané řady nevíme nic. Pro takovou situaci nemáme obecný návod, každá řada je individuální problém a vše závisí na naší zkušenosti, zkoušíme najít nějaký trik k určení její konvergence.
Někdy se dá použít jeden z následujících dvou testů.
Následující kritérium nám umožňuje vzít řadu, o které víme, že konverguje, a modifikovat ji bez ztráty její konvergence.
Věta (Abelovo kritérium).
Uvažujme konvergentní řadu∑ ak. Předpokládejme, že{bk} je monotonní a konvergentní posloupnost. Pak také řada∑ akbk konverguje.
Abelovo kritérium se dá získat z následujícího, obecnějšího kritéria.
Věta (Dirichletovo kritérium).
Uvažujme řadu∑ ak takovou, že jsou všechny její částečné součty omezené; to znamená, že existuje nějaké M takové, že pro všechny N máme
Předpokládejme, že {bk} je nerostoucí posloupost kladných čísel, která jde k 0. Pak řada ∑ akbk konverguje.
Pro příklady viz tento příklad a tento příklad v části Řešené příklady - Testování konvergence.
Tento test lze použít v širokém spektru situací, ale jedna konkrétní situace
stojí za bližší rozmyšlení. Všimněte si, že tento test také implikuje
Leibnizovo kritérium výše. Schválně si představme situaci jako v
předpokladech Leibnizova kritéria. Máme kladná čísla
bk, která jsou nerostoucí a jdou k nule. Teď z nich
vyrobíme alternující řadu, což se dá interpretovat následovně: Vytvoříme
řadu se členy
Právě jsme vysvětlili, proč Dirichletovo kritérium zobecňuje Leibnizovo kritérium, je ale zajímavé se k té situaci ještě vrátit a trochu se v ní pošťourat. Tvrdíme, že když začneme s kladnými čísly bk, která jsou nerostoucí a jdou k nule, pak nám Direchletovo kritérium umožňuje je modifikovat znaménky i jinými způsoby než tím alternujícím. A opravdu, předpokládejme, že členy ak jsou čísla −1 a 1, která jsou vybrána takovým způsobem, že se určitý vzor opakuje stále dokola (jakási periodická posloupnost). Pokud je v tomto vzoru stejný počet plusů a mínusů, pak mohou částečné součty zase nabývat jen několika hodnot, tudíž jsou omezené a Dirichletovo kritérium dává konvergenci. Toto je rozhodně významné vylepšení ve srovnání s dost speciálním Leibnizovým kritériem. Tuto sekci uzavřeme formální formulací tohoto zobecnění.
Fakt.
Uvažujme číslaak = ±1. Předpokládejme, že existujeT > 0 takové, žeakT+i = ai pro všechna přirozená čísla k a celá čísla i splňující 0≤ i < T. Nechťa1 + a2 + ... + aT = 0.
Předpokládejme, že
{bk} je nerostoucí posloupnost kladných čísel jdoucí k nule. Pak řada∑ akbk konverguje.