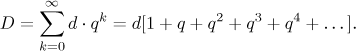
Je jich vlastně více, ale nejslavnější z nich je znám coby problém Achilla a želvy.
Achilleus byl velký řecký bojovník, jehož činy byly ještě donedávna známy každému vzdělanému člověku ve světě atlantské civilizace (tedy kultur s evropskými a středozemními kořeny). Mimo jiné byl hodně rychlý. A teď si představte toho bájného atleta, jak vidí želvu a z nějakého důvodu se ji rozhodne chytit (asi už mu došli lidští nepřátelé a nemá koho zabíjet). Všichni víme, že ji chytne, ale asi před 2 a půl tisíci lety přišel filosof Zénón z Eleje se zajímavou teorií, že tomu tak není.
Odůvodnil to takto. Achilleus vyběhne za želvou, ale ona ho vidí a začne "utíkat" pryč. Achilleus je samozřejme rychlejší a brzy doběhne na místo, kde želva původně byla, ale než se tam dostane, tak už se želva posune trochu dále. Tak Achilleus běží dál a brzy přijde na místo, kde želva byla, když doběhl na její původní pozici, ale ta želva už tam zase není, odběhla na pozici tři. A než se tam Achilleus dostane, je už želva na pozici čtyři. A tak dále a tak dále až do zblbnutí, což dokazuje, že Achilleus nikdy nechytí želvu.
Samozřejmě že se Zénón nesnažil naznačit, že Achilleus želvu nikdy nechytí. Řekové byli patrně první, kdo vážně studovali přírodu a používali na to matematiku (filosofové byli původně lidé, kteří se snažili pochopit, jak svět funguje, jacísi univerzální vědci). V té době ale nebylo jasné, zda je na to matika ten správný nástroj, diskutovali podstatu mnoha základních věcí a onen paradox byl součástí rozprav o podstatě pohybu. Někteří filosofové dokonce stále tvrdí, že tu pořád ještě zůstávají nevyřešené fundamentální problémy plynoucí z tohoto paradoxu. Jak se na to dívá matematik?
Označme jako d původní vzdálenost mezi Achillem a želvou. Nechť
q je poměr rychlosti želvy vůči rychlosti Achilla (číslo menší než
1). Je snadné nahlédnout, že když Achilleus doběhne na želvino původní
stanoviště, tak je nová vzdálenost mezi nimi rovna
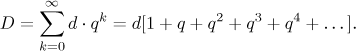
Toto je
geometrická řada, která pro
Jak dlouho to zabere? Nechť t je čas, který zabere Achillovi dostat se na první pozici želvy (takže t je rovno d děleno jeho rychlostí). Podobný argument jako výše ukazuje, že čas potřebný k překonání oné konečné vzdálenosti (rozdělené na nekonečně mnoho kousků) je
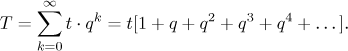
Zase dostáváme konečný čas. Tímto způsobem byl tento paradox vyřešen už okolo roku 200 př.n.l. Aristotelem.
Mimochodem, kdyby byl Achilleus dvakrát rychlejší než želva, pak by ta řada vyskytující se v obou vzorcích výše byla přesně řada
1 + 1/2 + 1/22 + 1/23 + 1/24 + ...,
kterou jsme diskutovali v úvodní sekci. Tento příklad tedy ukazuje, že sčítání takovéto řady odpovídá reálnému světu.
Zénón přišel s mnoha paradoxy. Osm z nich přežilo a jsou známy. O pěti se říká, že jsou snadno vyvratitelné, tři jsou poněkud těžší a slavnější. Jeden z těch tří jsme právě viděli, další dva jsou "dichotomický paradox" a paradox "letícího šípu". Všechny tři mají jedno společné téma. Ve fyzice (a jiných oborech) si často pomáháme tak, že komplikovanější děj rozložíme na menší a jednodušší kousky, které už umíme zvládnout (viz třeba tento příklad). Zenon chtěl upozornit na to, že to nemusí být až tak úplně samozřejmé a měli bychom to dělat opatrně, zvlášť pojem pohybu není až tak snadný, jak se zdá.
Z pohledu matematika (a snad každého praktického přírodního vědce) jdou už tyto paradoxy dávno pohřbeny, kalkulus na ně umí odpovědět a jeho metody pro nás evidentně fungují. Někteří filosofové ale nejsou přesvědčeni, kladou si třeba takovéto otázky: Možná nám ten čas vyšel konečný, ale jak může někdo zvládnout udělat nekonečně mnoho věcí a dostat se na jejich konec? Nevím jak vy, ale jako student jsem ke konci zkouškového období míval pocit, že jsem to zrovna dokázal.