Problem: Determine whether the following series converges absolutely.
![]()
Solution: To investigate absolute convergence we should take absolute value of the terms in the series, but they are all positive and thus the absolute value has no effect. Thus for this particular series, absolute convergence is equivalent to its convergence and we (hopefully) find out by applying tests for series with non-negative terms to it.
What test looks suitable? We know that since the terms feature only polynomials and roots, we do not get any help from the Root test and the Ratio test. In fact, evaluating the limits appropriate for these two tests would be rather tough due to the subtraction in terms, so it is good to know that there is no point in doing it.
What other tests are there? The idea of integrating the terms does not look too appealing, yet its just powers and roots, so it should not be impossible. The obvious unpleasantness of this approach suggests that we should keep it as the last resort, now we look at the last possibility, namely comparison tests.
When we scan the given series for parts that can be ignored, we quickly find that there is no simple answer here. One comparison by inequality is obvious, ignoring the second root, but we would make a substantial change in this way, which is usually a clear sign that we are too generous and such an estimate is no good. Indeed, we would get
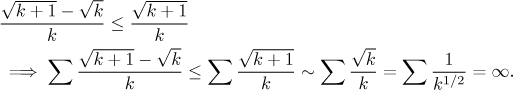
In the last step we argued that the "+1" does not make any difference
for large k, and so we can pass to a series that is divergent by
the
p-test, here
How about Limit comparison then? What happens when k is large? If we ignore the "+1" part on the top, then the two roots cancel out and we get 0. This is caused by the fact that the two roots have the same dominants that subtract, and in the section Intuitive evaluation in Sequences - Theory - Limits we reasoned that in such a case this intuitive approach fails. Thus it will not work this way. If we really want to know what our terms do when k is large, we have to get rid of the roots algebraically first.
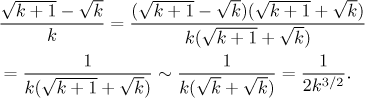
We have made our guess and now it is time to confirm it.
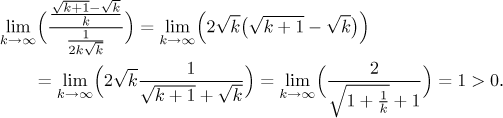
The guess is confirmed, now we know that
![]()
By the p-test, the test series on the right converges, and therefore by the Limit comparison test also the given series converges.
Conclusion: The given series is absolutely convergent.
For the sake of completeness we will now try the Integral test. Are the assumptions satisfied? The function that defines the terms is positive, but its monotonicity is definitely not obvious. We will look at the derivative.
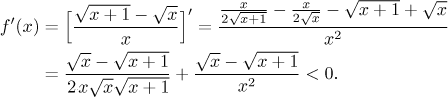
The function f is therefore decreasing on, say,
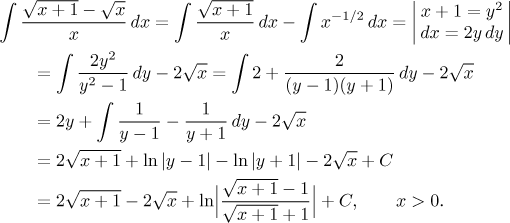
So we have the antiderivative and now we can pass to the definite integral. When evaluating the limit, there will be two problems. The logarithm will have an indeterminate ratio inside, but that is easy to handle by cancelling the highest power in the fraction, which is the root of x. The other part, the difference of roots, also gives an indeterminate expression, and for difference of roots we have the standard trick, namely getting rid of them algebraically. For more details on these tricks, see Limits in Functions - Methods Survey.
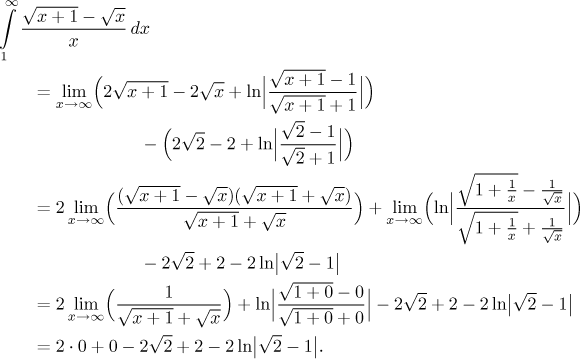
The integral converges, which confirms the convergence of the given series.