Problem: Investigate convergence of the following series. (Does it converge? If it does, then how?)

Solution: We have to check on convergence of the given series and also on its absolute convergence. We start with the former. The given series looks like it is alternating, but to confirm it we have to check that the logarithmic part is always positive. This is easy, for positive integers k the argument 1 + 1/k is greater than 1 and so the logarithm is positive.

Thus we indeed have an alternating series and we can try to use the Alternating series test. The numbers

b_k = ln(1 + 1/k)

form a decreasing sequence of positive numbers that goes to zero. By AST, the given series converges.

Now we will check on absolute convergence. We know that the logarithm is positive, so we have

We start with the Ratio test.

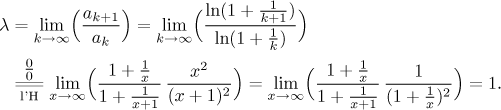
We have λ = 1, which is the indecisive case and the Ratio test does not help. Thus there is also no point in trying the Root test, since there we would also get the indecisive case ϱ = 1. This is actually fortunate, since the Root test would force us to evaluate a rather nasty indeterminate power.

What other test could help? We could try the Integral test, since the function ln(1 + 1/x) is both positive and decreasing on the interval [1,∞). We first try to find the indefinite integral, since this looks like a more complicated integral and we do not want limits to get in the way. Probably the best start is to get rid of the logarithm using integration by parts.

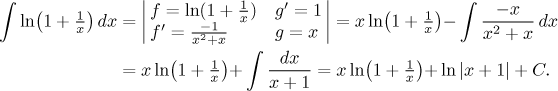
Now we pass to the appropriate improper integral. The limit will involve indeterminate product, we will handle it in the standard way.

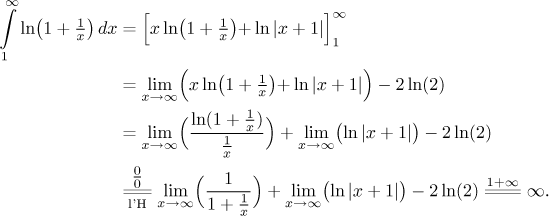
Since the integral diverges, also the series we investigate diverges, therefore the given series does not converge absolutely.

We determined that the series itself converges, but it is not absolutely convergent.
Conclusion: The given series is conditionally convergent.

We return to the series with absolute values and for the sake of completeness we will look at comparison tests. The only obvious estimate of logarithm is by a constant from above, say ln(1 + 1/k) < 2, but infinite sum of 2's is divergent and thus such a comparison is useless. We would need a tighter, less generous estimate, but no such estimate is generally known. Perhaps a better approach is to try limit comparison, that is, we ask ourselves the following question: When k is large, how do the terms look like?

An easier question is this: When x is positive and very small, how does ln(1 + x) look like? We can try to approximate it using its tangent line (see Derivatives - Methods Survey - Applications) and we get that

ln(1 + x) ∼ x.

When we use it in our case, we get a limit comparison that has to be confirmed.

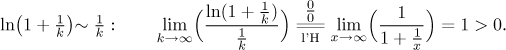
Our guess was justified, therefore we also have

This confirms that the given series is not absolutely convergent. Incidentally, the series on the right is the harmonic series whose divergence is well-known, for instance by the p-test.

Next problem
Back to Solved Problems - Testing convergence