Box "substitution"

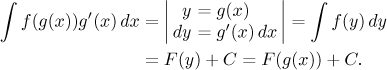
Substitution is a method that allows us to change variable in an integral using a chosen transformation formula, here we will pass from x to y. If the formula has the form y = g(x), then it is a direct substitution, an indirect substitution is given by h(y) = x, and a mixed substitution is given by a formula of the form h(y) = g(x). The simplest of them is the direct substitution, calculations go this way.

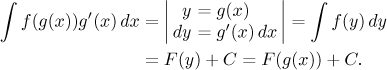
However, often it happens that although we start with the formula y = g(x), we use it also in modified forms, so the procedure effectively becomes closer to mixed substitution, in practice the differences tend to disappear. Thus it makes sense to show now a general algorithm for a mixed substitution, the direct and indirect ones will then be just special cases.

Algorithm for substitution.
Step 1. Choose a transformation formula h(y) = g(x).
Step 2. Deduce the corresponding transformation for differentials, h ′(y)dy = g′(x)dx.
That is, differentiate both sides of the equality and attach corresponding differentials.
If the substitution was direct, y = g(x), then differentials transform according to dy = g′(x)dx.
If the substitution was indirect, h(y) = x, then differentials transform according to h ′(y)dy = dx.
If the integral includes the expression g′(x)dx and apart from it, the variable x appears only as the expression g(x), go to the next step.
Otherwise, use the formulas from Step 1 and 2 to deduce other formulas that are needed for expressing x in the integral.
Step 4. Change the integral from the language of x to the language of y by replacing all appearances of x (including dx) using only the formulas deduced from the chosen transformation formula in previous steps and nothing else. No x can remain in the transformed integral. If this is not possible, then the chosen substitution cannot be done.
Instead of deducing new formulas in Step 3, sometimes it is possible to rewrite the integral into a form that fits the formulas that we already have from Steps 1 and 2.
Step 5. Evaluate the new integral, obtaining an antiderivative that uses y as variable. Then do the corresponding back substitution, that is, deduce a formula for y from the basic transformation formula (not needed when direct substitution is used) and substitute for y into the answer, thus passing back to the language of x.

Example: Consider the following calculation.

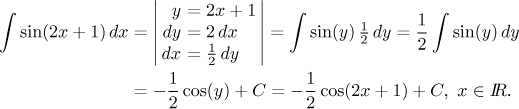
The given integral is not an elementary one, but it would become one if we could replace the term 2x + 1 with y. This inspires our choice of the transformation formula, but we cannot replace it yet. We need to replace both appearances of x and in order to replace dx one needs to deduce the appropriate formula (Step 2 above). Note that this formula comes only from our chosen transformation, the integral has no influence on it.

Only after we deduce dy = 2dx it is time to go back to our integral and see how it fits. The answer is that it does not fit well, since we do not have 2dx in our integral. Thus it is time to do Step 3, that is, try to rewrite our formulas to a more helpful form, in this case we would appreciate having an expression for dx. Fortunately, we were able to get it.

Thus we have the right formulas for replacement and we do the substitution. As expected, we obtained an elementary integral and solved it. At the end we did the back substitution and added the necessary parts: the constant C and specification of validity.

Instead of deducing new formulas it is sometimes possible to create needed expressions in the integral itself. Here it is easy.

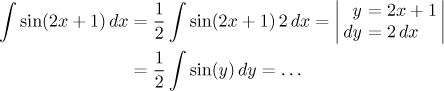
This example was extremely simple, in fact an experienced integrator would often write the answer right away, doing calculations in his head, but it shows the basic features of substitution. Before we pass to examples delving deeper into intricacies of substitution, we address an imporant question.

How to choose a substitution

In most cases we use substitution to simplify a composed function. In a typical case the variable appears in the form of some expression g(x) that is substituted into a function f. If we replace g(x) with just a letter y, the integral significantly simplifies. Thus we arrive at the direct substitution y = g(x). Some examples of substitutions that suggest themselves this way are here.

Therefore the first indication that a substitution might be a good idea is the presence of a composed function. However, that is just the first step. We know that success of substitution is determined by being able to transform all appearances of x, usually the biggest problem is the differential. So when we start thinking about some substitution y = g(x), we should ask whether there is also the term g′(x)dx in the integral. If it is there, then the substitution most likely succeeds.

So to sum it up, if the given integral involves a composed function, we look at the expression inside and check whether its derivative is next to dx. If the answer is yes, then this substitution should work. For instance, we would definitely use substitution y = g(x), dy = g′(x)dx with integrals like these:

After substitution they would become integrals of 1/y, yⁿ, sin(y), and e^y, respectively.

However, very often this is not the case. Then we have to ask whether we can at least rearrange things to fit. In many cases this is possible, in particular this is true for all linear substitutions y = Ax + B, dx = 1/Ady, see the example above. Using linear substitution we easily simplify integrals like these:

For instance, in the following integral the composed function clearly points to the linear substitution y = 2x − 1 and we now know that it will succeed, we just need to find a formula for x in the numerator.

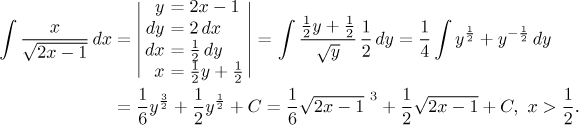
Other integrals where getting creative with substitution helps are shown here. However, experience says that if we need to create something more complicated next to dx, then it is a clear sign that this substitution may not be the best idea, because in the process of creating things we make the new integral complicated again. We show some examples here.

So far we discussed direct substitution. When do we pass to the mixed one? That is influenced by f, some functions would simplify if we put instead of y some suitable expression in them. There are several types of integrals where we know this to be a good idea, most notably those with roots, see the appropriate box above.

The same is true for indirect substitution, again we use it for specific types, see integrals with roots of quadratics above. The indirect substitution is easier to do, since we immediately get a formula for dx, but it frequently has troubles with back substitution and often one has to worry about the chosen formula being 1-1. Here it is really important to check on correctness of the answer.

Example: Consider the integral

It is an integral with a root of quadratics and the corresponding box recommends the indirect substitution x = sin(t) that should go through without any problem.

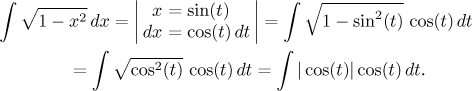
We have the first problem, we need to get rid of that absolute value. Do we know anything about the sign of cosine? This hangs on a question that is typical for indirect substitution, we need to talk about intervals. The original integral obviously exists on the closed integral from −1 to 1, the function is continuous there, but what about the new one? Indirect substitution requires that we choose some interval on which the sine function is 1-1 and that is mapped onto the interval [−1,1]. Candidates are obvious and depending on which we choose, the sign of the cosine there will be determined.

There is no reason to get creative, we decide on I = . There the cosine is non-negative and we can simply ignore the absolute value. We get an integral that belongs to the box on trig integrals, where the recommendation is to use an identity to reduce the power, then it is easy.

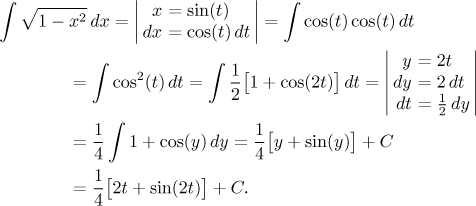
Now we need to do the back substitution, which is exactly the moment when we appreciate that sine is 1-1 on the chosen interval. Thus we can express t from the basic substitution formula using the inverse function.

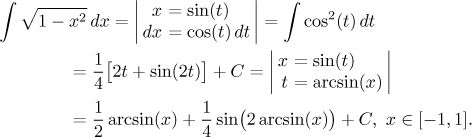
Note that if we chose for instance the interval that is shifted to the right by π, then the cosine would be negative, so we when evaluating the integral with t we would get the result with the opposite sign. On the other hand, we would also get a different formula for t, so in the end we would obtain the same answer, just with more work.

While the above answer is correct, it is also certainly very ugly. Since there were no trigonometric functions in the question, it is good manners to try to avoid them in the answer, too. There is nothing we can do with the solitary arcsin, but the second expression can be handled better; namely, before substituting into sin(2t) we will try to change it into into an expression featuring sin(t) = x only.

So we get (check that the answer is indeed correct):

Not very nice, but the best we can get. By the way, you would find this integral in most lists of integrals in math books.

Most problems in Solved Problems - Integrals feature substitution, we would point out this, this, this, this and this problem, in this problem you will see a nice mixed substitution and in this one a cute trick using substitution. A closer look at problems with integrating interval in indirect substitution can be found in the box integrals with roots of quadratics.

Next box: integration by parts
Back to Methods Survey - Methods of integration