Příklad: Rozviňte danou funkci v mocninnou (Taylorovu) řadu s daným středem.
![]()
Řešení: Arkus tangens není funkce, jejíž řadu bychom si pamatovali. Potřebujeme tedy najít nějaké spojení mezi touto funkcí a kvartetem, který si pamatujeme. Rozhodně z těchto čtyř funkcí nedostaneme arkus tangens algebraicky. Jedna možnost je použít Lagrangeův inverzní vzorec aplikovaný na arkus tangens coby interzní funkci k tangensu. Je to ale dost drsné (viz níže), takže si to necháme jako poslední zoufalou možnost.
Jak to vypadá s dalšími způsoby, jak funkce spojovat, třeba derivováním a
integrováním? Derivace arkus tangensu je
![]()
Teď použijeme geometrický rozvoj, všimněte si, že platí pouze pro
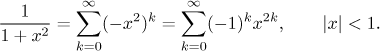
Abychom dostali arkus tangens, budeme integrovat. Jsou dvě možnosti. Jedna je integrovat pomocí určitého integrálu s proměnnou jako horní mezí (pak je dobré změnit proměnnou v našem rozvoji na t), což dává
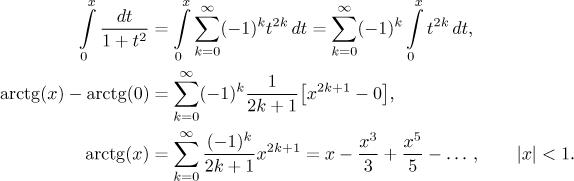
Druhá alternativa je použít neurčitý integrál:
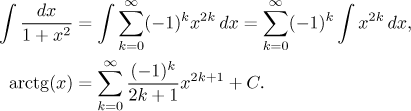
Potřebujeme určit C, ale to je snadné. Ona rovnost výše by měla
platit pro všechna x splňující
Poznámka: Jak bychom to řešili pomocí Lagrangeova inverzního vzorce? V našem případě dává
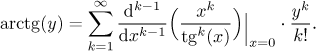
Derivace obecného řádu
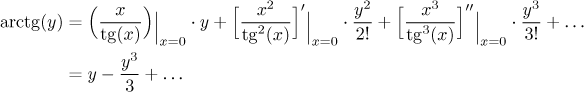
Zdá se, že se to shoduje s naším výsledkem, ale jít dál by byla ztráta času, už i ta druhá derivace byla dost hnusná.
Bonus: Zde ukážeme, jak rozvinout tangens pomocí toho, že je to podíl dvou funkcí se známým rozvojem, tedy použitím metody neurčitých koeficientů. Začneme tím, že si napíšeme standardní rovnost pro tangens a pak v něm nahradíme funkce řadami. Protože tu správnou řadu pro tangens ještě neznáme, napíšeme tam obecnou řadu se středem 0.
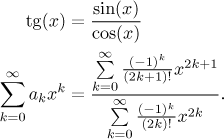
Teď vynásobíme jmenovatelem a pak řady přepíšeme dlouhým způsobem, abychom lépe viděli, co se děje.
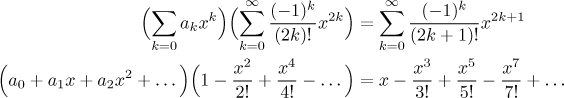
Když nalevo použijeme Cauchyho součin, tak uvidíme, jaké koeficienty jsou před jednotlivými mocninami xk, což se dá porovnat s odpovídajícími koeficienty napravo. Dostaneme rovnice
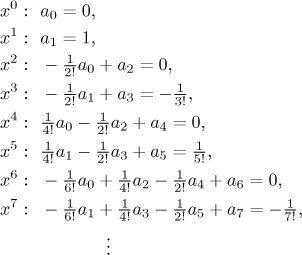
Vzor se zdá jasný. Indukcí určíme
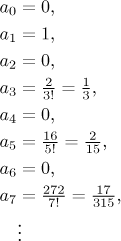
Vidíme v tom nějaký pravidelný vzor? Popravdě řečeno, ne. Taylorova řada pro tangens je samozřejmě známa, ale její koeficienty používají něco zvané Bernoulliho konstanta, což rozhodně není snadné spočítat (a upřímně řečeno, s tím, co se zde probralo, se k ní nemáme šanci dostat). Metoda neurčitých koeficientů nám alespoň umožnila najít začátek tohoto rozvoje tangensu.
![]()