Příklad: Vyšetřete konvergenci následující posloupnosti funkcí:
![]()
Řešení: Nejprve se podíváme na bodovou konvergenci. Budeme považovat x za parametr a spočítáme limitu vzhledem ke k. Vidíme, že typ této limity záleží na hodnotě x:
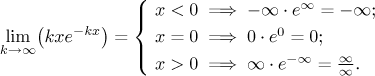
Vidíme tedy, že tato posloupnost diverguje pro záporná x. Pro kladná x použijeme l'Hôpitalovo pravidlo (připomeňme že x je parametr, takže teď předstíráme, že k prochází reálnými čísly, a derivujeme vzhledem k tomuto k).
![]()
Závěr: Daná posloupnost konverguje k funkci
Jak je to se stejnoměrnou konvergencí? Začneme zkoumáním rozdílu mezi f a jednou konkrétní fk na právě zjištěném oboru konvergence.
![]()
Toto globální maximum zjistíme obvyklým způsobem, identifikujeme podezřelé body a porovnáme hodnoty/limity v těchto bodech (teď je k pevná parametr a používáme x jako pracovní proměnnou).
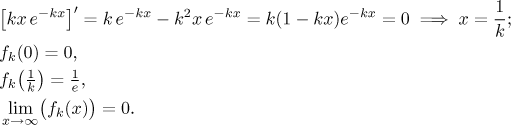
Vidíme, že
![]()
Takže vidíme, že vzdálenost mezi limitou f a členy posloupnosti fk zůstávají velké, když se na ně díváme globálně na celém oboru konvergence, tudíž na této množině nemáme libovolně dobré aproximace f pomocí fk. Jinými slovy, bodová konvergence, kterou jsme předtím našli, není stejnoměrná. Počítačový výstup souhlasí s naším teoretickým výsledkem.
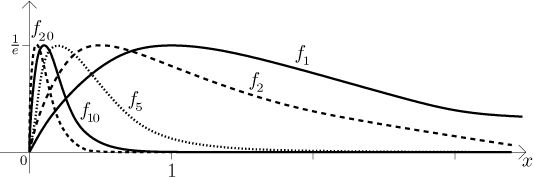
Pokud zvolíme nějaké kladné x, tak v tomto bodě jdou funkce
fk k 0 (a zdá se, že docela rychle). Na druhou
stranu, vidíme tam hrbol konstantní výšky klouzající doleva směrem k počátku
(určili jsme, že maximum k-té funkce se nachází v bodě
Zvolme nějaké a > 0, uvažujme množinu
![]()
Snadno se ověří, že Mk jdou k 0 pro k jdoucí do nekonečna, což dokazuje stejnoměrnou konvergenci na množině M.
Závěr: Daná posloupnost konverguje k funkci 0 stejnoměrně
na každé množině typu