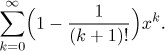
Příklad: Sečtěte následující mocninnou řadu.

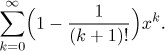
Řešení: Neznáme nějakou řadu, jejíž koeficienty by se skládaly z více částí, takže tím musíme začít. Jsou v zásadě dva způsoby, jak na tento problém. Mohli bychom zkusit přepsat každý koeficient jako jeden člen a pak by se vidělo. Druhá možnost je rozdělit řadu na dvě. Co je lepší volba? Když si představíme výsledek spojení těch dvou částí koeficientu (pomocí společného jmenovatele), tak vidíme, že s něčím takovým si rozhodně nechceme nic začínat. Na druhou stranu jsou jednotlivé části v rozdílu opravdu pěkné, takže tento druhý přístup je rozhodně lepší.

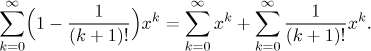
První řada se sčítá snadno, protože je to geometrická řada.

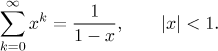
Teď se podíváme na druhou řadu. Potřebujeme ji převést na řadu, kterou už známe. Protože obsahuje všechny členy, tak sinová či kosinová řada nevypadají jako dobrý nápad, a protože se neumíme zbavit faktoriálů, zbývá nám řada, která má v sobě všechny mocniny a faktoriály: exponenciální řada.

Jediný problém je, že ve jmenovateli nemáme zrovna k!. To se dá napravit dvěma způsoby. Za prvé, lze posunout index.

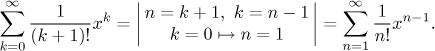
Teď máme dva problémy, mocnina a první index se neshodují. Mocnina se změní snadno, když řadu vydělíme a vynásobíme výrazem x, chybějící první člen exponenciální řady se doplní pomocí triku přičtu-odečtu. Jako obvykle místo n píšeme tradiční k. Protože používáme jen algebraické operace, můžeme to zapsat snažším způsobem - jako řetězec rovností.

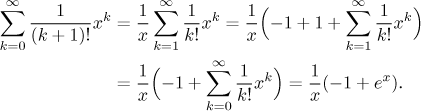
Máme malý trablík v 0, ale to není problém. Otázka zní "sečtěte řadu", takže prostě vrazíme 0 do dané řady a tím dostaneme odpověď.
Závěr:

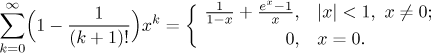
Alternativa:
Jak ještě můžeme zpracovat druhou řadu? Potíže dělá faktoriál z k + 1, raději bychom měli faktoriál k. To se tam objeví, pokud vytvoříme k + 1 v čitateli, na to máme trik: derivování. Jmenovitě bychom potřebovali derivovat x^k+1, což si snadno vyrobíme tak, že řadu vynásobíme x. Všimněte si následujícího: U prvního řešení výše jsme začali danou řadou a řetězcem rovností ji změnili do tvaru, který jsme už uměli sečíst. Zde to není možné, protože chceme derivovat, tedy chceme přejít k jinému objektu, který se původní řadě (či nějakému jejímu předpisu) nerovná. Musíme tedy použít jiný zápis, ten s f.

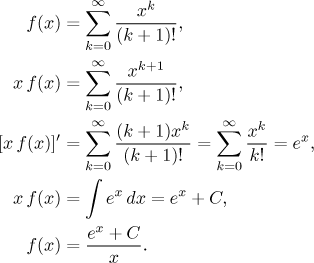
Kolik je C? Obvyklý trik je dosadit za x nějaké číslo do obou stran poslední rovnosti, a připomeňme, že f zde zastupuje danou řadu. Když se na ni podíváme, vidíme, že jediné x, ve kterém ji umíme vypočítat, je x = 0, ale toto číslo zase nejde dosadit do výrazu napravo. Dalo by se to dosadit do předposledního řádku, jeětě než jsme vydělili tím x? Zase ne, ale z jiného důvodu. Připomeňme, že rovnici můžeme vynásobit číslem jen v případě, kdy není nula - ale přesně to děláme na druhém řádku, když je x = 0. To znamená, že předvedené řešení už od druhého řádku funguje jen pro nenulová x.

Abychom se z této situace dostali, musíme použít znalosti o funkcích. Na předposledním řádku máme rovnost dvou funkcí, která platí na intervalu s výjimkou bodu uprostřed, jmenovitě se rovnají na nějakém prstencovém okolí bodu 0. Proto tam také ty dvě funkce musí mít stejnou limitu, a protože jsou spojité, musí se také rovnat v bodě 0. Závěr tedy je, že předposlední rovnost můžeme použít i pro x = 0. Když to tam dosadíme, dostaneme C = −1, proto máme stejný vzorec jako u prvního řešení.

Další příklad
Zpět na Řešené příklady - Řady funkcí