Odmocninové a podílové kritérium

Jeden typ řady známe velice dobře - geometrickou řadu. Může proto pomoci, pokud zjistíme, že daná řada je podobná geometrické řadě. Odmocninové kritérium a podílové kritérium jsou v zásadě dva způsoby, jak takovou podobnost rozeznat. Nejprve ukážeme populárnější typ těchto dvou testů - limitní verzi.

Věta (odmocninové kritérium - limitní verze).
Uvažujme řadu ∑ a_k splňující a_k ≥ 0 pro všechna k. Předpokládejme, že limita

konverguje.
• Jestliže ϱ < 1, pak daná řada konverguje.
• Jestliže ϱ > 1, pak daná řada diverguje.

Říká se tomu také D'Alambertovo kritérium. Proč to takto funguje? Limitní výsledek ríká, že pro opravdu velká k v zásadě máme

Takže řada, která splňuje předpoklady tohoto testu, opravdu vypadá jako geometrická řada (pro velká k, tedy na svém konci, ale víme, že konvergence se rozhoduje na konci řady). Teď by měl být závěr jasný (nebo alespoň uvěřitelný). Co s případem ϱ = 1? Odmocninové kritérium nedává žádný závěr. V tomto případě jsou členy řady víceméně jako 1^k. Odpovídající geometrická řada je divergentní, ale jde o hraniční případ mezi konvergencí a divergencí. Protože členy dané řady nejsou přesně rovny 1^k, ale mohou být o trochu větší či menší, vyplývá z toho, že konvergence závisí na tom, jak přesně se členy řady pohybují okolo čísla 1, proto je to vysoce individuální a nedá se pro takový případ očekávat obecné pravidlo.

Věta (podílové kritérium - limitní verze).
Uvažujme řadu ∑ a_k splňující a_k > 0 pro všechna k. Předpokládejme, že limita

konverguje.
• Jestliže λ < 1, pak daná řada konverguje.
• Jestliže λ > 1, pak daná řada diverguje.

Také se tomu říká Cauchyho kritérium. Proč to tak funguje? Limitní výsledek říká, že pro opravdu velká k v zásadě máme

Zde to není tak jasné jako u odmocninového kritéria. Pro jednoduchost předpokládejme, že ona aproximace v limitě funguje pro všechna k, ne jen pro ta velká, a pak můžeme udělat toto:

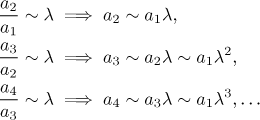
Všimněte si, že zase případ lambdy rovné 1 je nerozhodnutý. Zde ale může pomoci pokročilejší test, viz Raabeho kritérium v sekci Teorie - Testování konvergence - Další kritéria.

Příklad: Vyšetřete konvergenci řady .

Použijeme odmocninové kritérium.

(Pro limitu výrazu k^1/k viz Fakt níže.) Protože ϱ < 1, daná řada konverguje.

Zkusíme tento závěr potvrdit nezávisle podílovým kritériem.

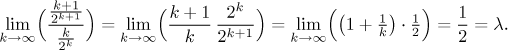
Protože λ < 1, daná řada opravdu konverguje. Všimněte si, že když jsme počítali limitu, tak jsme výraz rozdělili do skupin se členy stejného "původu"; to je typické a obvykle to velice pomůže.

Všimněte si také, že ony dvě konstanty z odmocninového kritéria a podílového kritéria vyšly stejné. To je vždy pravda (pokud mohou být použity oba testy) a není to vůbec překvapující. Každý test v zásadě odpovídá na otázku "jaké geometrické řadě se podobá ta daná," a tatáž řada nemůže být podobná zároveň dvěma různým geometrickým řadám. Teoreticky je odmocninové kritérium "silnější" v následujícím smyslu: Jestliže limita pro λ konverguje, pak nutně také limita pro ϱ konverguje (a ke stejnému číslu). Takže teoreticky vzato, pokud zabere podílový test, pak můžeme vždy místo toho použít i odmocninový test. Na druhou stranu existují řady, u kterých limita pro ϱ konverguje, ale limita pro λ ne, a tak nelze použít podílové kritérium. Zde ovšem hovoříme o teoretické konvergenci, hledání limit v praxi může být něco jiného. Jsou případy, kdy je použití podílového kritéria snadné, ale limita v odmocninovém kritériu je opravdový zabiják.

Při používání odmocninového kritéria se často používá fakt, že k-tá odmocnina z k jde k 1. To se dá zobecnit následovně.

Fakt.
Uvažujme nenulový polynom p(x). Pak

Z praktického pohledu to znamená, že když je řada založená na polynomech, tak nám obvykle odmocninové a podílové kritérium nedají informaci o její konvergenci. S oběma kritérii si naopak velice dobře rozumí řady s výrazu jako 2^k, jak už jsme viděli výše. Pro rady o nejlepší volbě testu viz Přehled metod - Testování konvergence.

Limitní verze obou testů, které jsme viděli výše, se snadno používají, ale nejsou nejsilnější možné. Jsou případy, kdy selžou ne kvůli výsledku 1, ale už než se k němu dostaneme. Víme, že ne každá posloupnost má limitu, takže se může stát, že dokonce ani nedostaneme žádné ró či lambdu. Ukážeme dva způsoby, jak to napravit.

Existuje obecnější pojem limity, takzvaná "limes superior". Je známo, že každá posloupnost {c_k} má "limsup", takže tento pojem je spolehlivější; pokud navíc ona posloupnost konverguje, tak se normální limita a limsup shodují. Dá se to použít v oněch kritériích? Ukáže se, že v odmocninovém kritériu stačí dát "limsup" namísto "lim" a všechno dál funguje. To je určitě užitečné a v některých knihách najdete tento test v tomto tvaru.

Na druhou stranu, pouze první tvrzení - to o konvergenci - se dá v podílovém kritériu udělat pomocí limsup. Pořád je to ještě užitečné, ale už ne tak elegantní. Pro přesná tvrzení viz tato poznámka.

Asi nejelegantnější a zároveň nejobecnější verze těchto testů dávají přednost individuálnímu pohledu na jednotlivé členy, bez použití nějakého limitního pojmu.

Věta (odmocninové kritérium).
Uvažujme řadu ∑ a_k splňující a_k ≥ 0 pro všechna k.
• Jestliže existuje ϱ < 1 a celé číslo N takové, že pro všechna k > N, pak daná řada konverguje.
• Jestliže pro nekonečně mnoho k, pak daná řada diverguje.

Jaký případ zůstává nerozhodnut? Když jsou výrazy a_k^1/k striktně menší než 1, ale blíží se k 1 libovolně blízko.

Věta (podílové kritérium).
Uvažujme řadu ∑ a_k splňující a_k > 0 pro všechna k.
• Jestliže existuje λ < 1 a celé číslo N takové, že pro všechna k > N, pak daná řada konverguje.
• Jestliže existuje celé číslo N takové, že pro všechna k > N, pak daná řada diverguje.

Pokud vás zajímá vztah mezi tímto "nerovnostním" přístupem a "limsup" přístupem, podívejte se na tuto poznámku.

Pro další informace viz Odmocninové kritérium a Podílové kritérium v části Přehled metod - Testování konvergence a také Řešené příklady - Testování konvergence. Jmenovitě, typická použití odmocninového kritéria se najdou v tomto příkladě, tomto příkladě, tomto příkladě a tomto příkladě, podívejte se také na tento příklad. Pro podílové kritérium se podívejte na tento příklad, tento příklad, tento příklad, tento příklad a tento příklad, zkuste také tento příklad.

Poznámka o obecných řadách: Jestliže daná řada ∑ a_k nemá členy se stejnými znaménky (nejsou buď všechna kladná nebo všechna záporná), pak lze odmocninové kritérium a podílové kritérium aplikovat jen na verzi s absolutní hodnotou ∑ |a_k|. Jestliže ϱ < 1 (nebo λ < 1), pak řada ∑ |a_k| konverguje a proto také automaticky řada ∑ a_k konverguje (viz Absolutní konvergence v části Teorie - Úvod).

Jestliže ϱ > 1 (nebo λ > 1), pak řada ∑ |a_k| diverguje. Obecně nám to neříká nic o původní řadě ∑ a_k, ale v tomto speciálním případě se dá divergence přesunout na původní řadu následující úvahou.
Je snadné ukázat, že jestliže ϱ > 1 (nebo λ > 1), tak |a_k| jde do nekonečna, což mimo jiné znamená, že a_k nejde k nule a tudíž (podle nutné podmínky) řada ∑ a_k diverguje. Touto úvahou vlastně vzniknou obecné verze těchto dvou kritérií, ty už ale patří do sekce Konvergence obecných řad.

Srovnávací kritéria
Zpět na Teorie - Testování konvergence