Problem: Investigate convergence of the following power series:

Solution: Is this really a power series? Actually, it is, we can rewrite it as

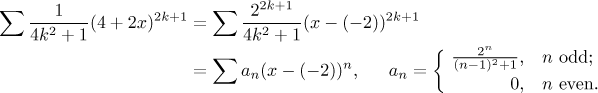
We see that the center of this power series is a = −2. We can use the standard approach, we start with determining the radius of convergence. Note that people who prefer to use the Theorem have it harder now, since they have to deal with those unpleasant coefficients a_k. The alternative way, simply applying a suitable test to the given series (see the first Remark in the previous problem), has no such problem and therefore we will use it. Here we go, as usual the Root test should work well.

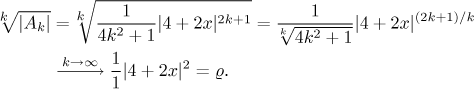
We used notation A_k for terms of this power series, since "a_k" (that you usually find in the Root test) is used for coefficients in the context of power series. In the denominator we used the fact that the k-th root of a polynomial always goes to 1.

We know that the series converges absolutely if rho is less than one, thus the condition is

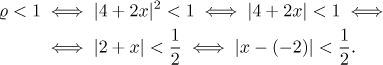
The radius of convergence is R = 1/2.

The interval of convergence is therefore at least

(−2 − 1/2,−2 + 1/2) = (−5/2,−3/2).

What is unclear is the status of endpoints, we need to check on them individually.

Endpoints:
x = −5/2: We substitute into the given series and obtain the series

What test do we use? Since the terms are not positive, we cannot use the usual tests. The natural choice here is the Alternating series test with

The sequence {b_k} is positive, decreasing and tends to zero, consequently the series in question converges.

x = 4: We substitute into the given series and obtain the series

What test do we use? This series is a prime candidate for some comparison. Would plain comparison test do? We can naturally estimate

and the series on the right is convergent (see the p-test). Thus by the comparison test, the series we investigate converges.

Thus both endpoints belong to the region of convergence, the above calculations show that we also have absolute convergence there.

Conclusion: The given series has the center a = −2 and radius of convergence R = 1/2. Its region of absolute convergence and region of convergence is [−5/2,−3/2].

Next problem
Back to Solved Problems - Series of functions