Problem: Investigate convergence of the following power series:

Solution: We see that the center of this power series is a = 0. (Indeed, x^k = (x − 0)^k.) We can use the standard approach and start with the radius of convergence, but we hit a snag right away. The coefficients of this series are so ugly that they are pretty much impossible to work out (in reasonable time) in the Root test or the Ratio test. Situation becomes much easier if we split this series into two and find the radius of convergence for each one separately. Then we will try put it together.

1. We investigate absolute convergence of

Here the usual choice - the Root test - is not very wise due to that factorial, we prefer to use the Ratio test.

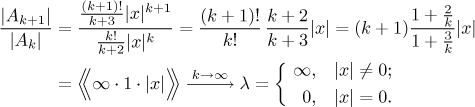
We know that the series converges absolutely if lambda is less than one, which here happens exactly if x = 0. This implies that the radius of convergence of the first series is R₁ = 0.

2. We investigate absolute convergence of

Here both of our favorite tests would work quite well, so to have some variety we will try the Root test.

We know that the series converges absolutely if rho is less than one, which here happens exactly if |x| < 3. This implies that the radius of convergence of the second series is R₂ = 3.

Since we know that the radius of convergence of a sum of two series is given by minimum of their individual radii (assuming that they are not equal, which is our case), we conclude that the radius of convergence of the given series is R = 0.

Thus the interval of convergence is [0-0,0+0] = {0} and there are no endpoints to check.

Conclusion: The given series has the center a = 0 and radius of convergence R = 0. Its region of absolute convergence and region of convergence is {0}.

Remark on radius: Why do we take when adding two series with distinct radii o convergence the smaller one? Assume that the radii are R₁ < R₂. We begin at the center of these two series and when we start moving out, we are first closer than R₁. There both series are convergent and thus also their sum converges. Its radius of convergence is therefore at least R₁.

Then we move further out, and when we are in the annulus between radii R₁ and R₂ then one series converges and the other diverges, thus their sum is divergent on this region. According to the theorem on behavior of radius of convergence, it means that the radius of convergence of this sum cannot be more than R₁.

If we move still further out, beyond R₂, then both series are be divergent and in general it could happen that their reasons for divergence would cancel out in the sum. However, this is not possible with power series. We know that for them convergence at some point necessarily means also convergence on the disc reaching up to that point, therefore we convergence cannot pop up anywhere beyond that annulus of divergence.

We also see that if the two radii were equal, then there would be no region of guaranteed divergence and thus there would be nothing to prevent situation when outside of the radius R₁ = R_@ two divergent power series add up to a convergent one. And this can indeed happen, then the radius of convergence of the sum is larger then the minimum of radii of convergence of the individual summands.

Next problem
Back to Solved Problems - Series of functions