In the previous section we saw that it is usually very difficult to find the precise sum of a convergent series. The obvious idea is to try to approximate it by summing up not all (that is, infinitely many) terms, but only the first few (thousand, million,...). How good is such approximation? This question is actually deeper than it seems.
Assume that we are given a series and we ask a computer to sum up its first zillion terms. We get the total 1000. What are we to think of this number? Is the series divergent (say to infinity), but slowly so we only got to 1000, but eventually we would get arbitrarily much? Or is it convergent? If yes, how close to its sum is that 1000? Obviously such questions cannot be answered. There are some tricks, but none of them really reliable. Please check out the section Numerical evaluation in Sequences - Theory - Applications for more insight; it is about sequences, but we know that we sum up a series by investigating the sequence of its partial sums, so it is very relevant (in fact the key example there uses series).
In order to get at least some answers we have to restrict ourselves to convergent series. We start by formulating the question we will want to answer.
Consider a convergent series
![]() ak.
ak.![]() . If we replace
the sum of the series by this partial sum, what is the error? That is, we
define the remainder
. If we replace
the sum of the series by this partial sum, what is the error? That is, we
define the remainder
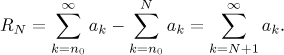
What can we say about it? Note that if the given series is not convergent, then such a difference does not even make sense. This brings us to our first observation. While deciding that a series is convergent without knowing where it converges (which is what we do most of the time in mathematics) may seem rather futile, we see that it is in fact a prerequisite for approximation of such sums using computers. Only if we prove that a series converges it starts making sense to do some numerical calculations.
However, even if we prove that a given series converges, we so far did not advance in the problem of knowing how close is the zillion-long summation to infinite summation. One option here is to get some help from the Integral test. The estimate that we show at the end of that section can be restated as follows. If ak in fact comes from some non-increasing and positive function f, then

This is not quite what we need, since many series do not satisfy the rather
strict requirements of this estimate. However, we rarely need to know the
error precisely, we are usually happy with an upper estimate. Thus we can
start relaxing the above situation. First, we do not really need all terms
of the series to be positive, since to get an upper estimate we may pass to
absolute value. However, then the resulting function
Fact.
Consider a serieslet ak,
N > n0. Assume that g is a non-increasing function such that|ak| ≤ g(k) for allk > N. Then
This sounds swell, but it is not as useful as it might seem, since not every function g that we cook up can be reasonably easily integrated. Still, sometimes it does help.
There is one case when we have a very simple and also very useful estimate for the error of approximation - when we deal with an alternating series.
Fact.
Consider a series∑ (−1)kbk, wherebk > 0 and{bk} forms a decreasing sequence tending to 0. Then we have
| R N | ≤ bN+1.
The assumptions of this theorem make more sense when compared with Alternating series test.
Note that here we asked how large the error
For examples see Methods Survey - Summing up series and Solved Problems - Summing up series, namely this problem and this problem.
Absolute convergence
Back to Theory - Introduction to
Series