Šuplík "substituce"

Substituce samotná zřídka vyřeší příklady, ale používá se k jejich zjednodušení a k přesunu problémů z jednoho místa na jiné. Je to vlastně obecná metoda. Základní myšlenka substituce pro posloupnosti je následující: Máme posloupnost {a_n}, ve které je n vždy uvnitř určitého výrazu, nazvěme jej f (n). Chceme najít limitu této posloupnosti. Jestliže výraz f (n) splňuje určité předpoklady (které jsou rozumné a přirozené), můžeme tento výraz nahradit novým písmenem (řekněme m) a dostaneme jednodušší příklad.

Začneme velice jednoduchým příkladem: Najděte

Protože se výraz 2n² objeví všude, kde máme n, můžeme tomuto výrazu dát nějaké jméno, řekněme m. Dostaneme novou limitu:

Ačkoliv to moc nepomohlo, příklad je v zásadě stejný (takže metody, kterými jej budeme řešit, budou v zásadě stejné), tato nová lmita vypadá mnohem snadněji a výpočty budou nejspíše jednodušší.

Poznámka: náhrada 2n² písmenem m nebyla tak jednoduchá, jak to vypadalo, bylo za tím víc, než je na první pohled patrné. Mimo jiné si všimněte, že nová limita má napsáno m→∞ pod značkou "lim". To má smysl, v novém výrazu nejsou žádné n, takže by značení mělo sedět. Nemůžeme ale jen tak změnit písmena, tato změna musí být založena na substituční rovnici m = 2n². Přesně řečeno, musíme ověřit, že jestliže n→∞, pak opravdu m = 2n²→∞.

Teď jsme připraveni formálně formulovat požadavky zajišťující, že substituce m = f (n) bude fungovat. Za prvé, čísla f (n) musí být celá pro celá čísla n. Za druhé, posloupnost {f (n)} musí jít do nekonečna pro n jdoucí do nekonečna. Pokud je toto splněno, můžeme změnit limitu z jazyka n na m. Všechny výskyty f (n) nahradíme m, musíme také změnit n na m v limitním symbolu.

Substituci lze ovšem také použít v obecnější situaci, zvolenou substituční rovnost m = f (n) můžeme použít k nahrazení jiných výrazů s n než jen f (n). Obecná substituce (pro limity posloupností) funguje takto:

Substituce:
Krok 1. Rozhodneme se, jaký výraz f (n) by měl být nahrazen, čímž určíme základní substituční rovnost m = f (n).
Krok 2. Ověříme, že jestliže je n přirozené číslo, pak také m = f (n) je celé číslo, a že m→∞ pokud n→∞.
Krok 3. Použijeme rovnost m = f (n) k nalezení příslušného vzorce pro n, popř. pro další výrazy objevující se v posloupnosti. Tyto výpočty se tradičně dělají mezi svislými čárami (viz následující příklad).
Krok 4. Transformujeme danou lmitu do nového jazyka m. Všechny výskyty n musí být nahrazeny, v dané posloupnosti nahrazujeme pomocí rovnosti m = f (n) a vzorců z nich odvozených, v obrázku "lim" prostě napíšeme m namísto n.

A to je všechno.

Poznamenali jsme, že nový limitní problém je v zásadě stejného typu, jako ten původní, substituce jej jen udělá jednodušším na zápis (což samotné často stojí za to). Jsou ovšem problémy, kde substituce pomůže ještě víc, jako například v následujícím příkladě.

Příklad: V tomto příkladě použijeme substituci k přesunu sčítání ze jmenovatele (kde s ním nic nenaděláme) do čitatele, kde si s ním algebra poradí. Všimněte si, jak substituci zapíšeme. Zápis vzorců mezi svislé čáry není standardní, ale je docela rozšířený. Jako obvykle také dáme poznámky mezi dvojité lomené závorky.

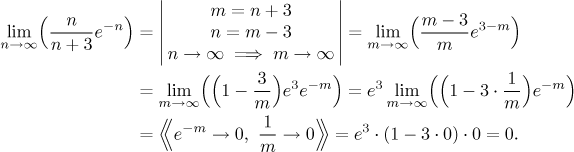
Všimněte si, že jsme vytáhli e³ z limity, protože je to multiplikativní konstanta a tedy ji lze vytknout, čímž je limita jednodušší.

Poznámka: Tuto metodu lze také použít při hledání limity funkcí. Vlastně když počítáme limitu posloupnosti, často používáme metody z teorie funkcí (viz Posloupnosti a funkce v části Teorie - Limita). Proto také není až tak nutné vyžadovat, že výraz f (n) dává celé číslo a jde do nekonečna. Když pak ale uděláme substituci, dostaneme limitu funkce, ne posloupnosti. Získaná odpověď pak také platí pro posloupnost. Ukážeme to na jednoduchém příkladě:

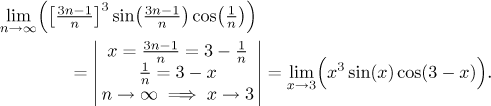
Měli bychom vlastně být schopni najít limitu přímo, ale chtěli jsme ukázat, jak substituce funguje. Všimněte si, že kdybychom to potřebovali, můžeme spočítat, že n = 1/(3 − x), a použít to. Všimněte si také, že x→3^- (x jde k 3 zleva; někdy je potřeba to vědět).

Další šuplík: 1/0
Zpět na Přehled metod - Limita