Numerické výpočty

S posloupnostmi se toho nedá numericky (typicky na počítači) dělat mnoho. Je evidentně nemožné zkontrolovat nekonečně mnoho určitých věcí jednu po druhé (jak to dělá počítač) v konečném čase, takže například nejde zkontrolovat nekonečně mnoho následných párů k potvrzení či vyvrácení určitého druhu monotonie. Totéž platí o omezenosti.

Jak je to s limitou? Je možné použít počítač k zjištění, zda daná posloupnost má limitu, a k jejímu nalezení? Bohužel, obecně to nejde, zase z toho důvodu, že počítač neumí zkontrolovat nekonečně mnoho čísel. Přesto jsou počítače často v této oblasti používány, obvykle se doufá, že naše problémy jsou dost pěkné na to, aby tak šly řešit.
Typický postup, který studenti aplikují na danou posloupnost, vypadá následovně: Začnou dosazovat čísla za n, nejprve menší, pak větší a větší, a sledují, co dělají výsledky. Pokud například stále rostou, student odhadne, že daná posloupnost roste do nekonečna. Když na druhou stranu ani pro velké hodnoty n posloupnost příliš neroste a moc se nemění, student si tipne, že posloupnost konverguje a že to číslo, které se stále objevuje, bude víceméně limita.

Typický počítačový program k hledání limit opravdu pracuje tímto způsobem. Často se používá tato metoda:

Vyber velké číslo N, dosaď jej do posloupnosti. Pak dosaď N +1. Jestliže a_N a a_N+1 začínají stejnými platnými číslicemi, pak tyto číslice asi budou dobře a jsou nejlepším odhadem pro limitu.

Někdy se pro jistotu srovnává N-tý člen s (N +10)-tým členem, nebo N-tý člen s (N +1000)-tým členem, je možné také zkusit srovnat N-tý člen a (2N)-tý člen a podobně.

Bohužel, ani jedna z procedur zde naznačených nefunguje spolehlivě. Je to způsobeno několika faktory. Jedním je fakt, že čísla, která dosazujeme, jsou omezená. Například do typické kalkulačky nedáte čísla větší než 10 umocněno na 99. Máme už teď nějakou zkušenost s posloupnostmi a hravě si umíme představit posloupnost, která je dokonce konstantní na svých prvních 10⁹⁹ členech a pak udělá něco divokého. Je jasné, že se o tom nedozvíte pomocí kalkulačky, která tak velká čísla neumí zpracovat. Další možný důvod pro špatný odhad pomocí kalkulačky je, že posloupnost má sice něco za lubem, ale dělá to tak pomalu, že si toho nevšimneme. Pokud chcete vidět pěkný příklad, pro který onen trik s porovnáváním následujících (či více méně následujících členů) selže, podívejte se na tuto poznámku.

Přesto se s touto procedurou často setkáváme. Proč? Protože není nic lepšího. Když potkáme posloupnost, doufáme, že to není jedna z těch bláznivých, použijeme triky popsané výše a doufáme, že jsme se o mnoho neminuli. Tedy, tak to děláme, pokud neumíme problém vyřídit teoreticky. V následujících sekcích dokonce ukážeme situace, kde nás zajímá právě numerický a ne teoretický přístup.

Numerický přístup je nejspolehlivější, pokud o dané posloupnosti také něco víme teoreticky neboli najisto. Dá se například dokázat, že pro určité typy posloupností ten trik s následujícími členy opravdu funguje.

Možná teď namítnete, že předchozí příklad - a vůbec celá myšlenka - jsou založeny na tom, že posloupnost může mít nějakou vlastnost, která se vyskytne hodně daleko, a pozorovatel nezkontroluje dostatečně mnoho členů, aby ji nakonec viděl. Kdyby byl pozorovatel více trpělivý, určitě by se nakonec dočkal. Jenže v tom je právě problém. Posloupnost je nekonečná, může si tedy dovolit čekat, než začne blbnout; zkontrolujete ji až po n = 10¹⁰⁰, co když posloupnost něco vyvede až potom? Seženete si superpočítač, zkontrolujete ji až po n = 10¹⁰⁰⁰, ale stejně si nemůžete být jistý, že něco nevyvede později.

Takové příklady jsou ovšem vzácné a můžete doufat, že o ně nezakopnete. Bohužel je ale ještě další důvod, proč má výpočetní technika problém s výpočtem limit, dokonce i docela jednoduchých, ten se týká zaokrouhlovací chyby a nedá se mu vyhnout. Podívejme se na následující problém:

To je velice pěkná posloupnost a je lehké ukázat pomocí příslušných triků, že konverguje k nekonečnu; nejprve se zbavíme odmocnin (viz šuplík "rozdíl odmocnin") a pak zkrátíme mocniny (viz šuplík "polynomy a podíly s mocninami").

Co se stane, když zkusíme spočítat členy této posloupnosti na kalkulačce?

n:	10	100	500	1000	10,000	1,000,000
an:	4.999	50	250	500	0	0

Jaký závěr byste udělali na základě této tabulky? Že tato posloupnost konverguje k nule! Skončili jsme, když jsme dosadili za n milion, ale dostali bychom nulu pro libovolná větší čísla. Jak je to možné?

Když si kalkulačka nebo počítač zapamatovávají reálné číslo, tak si pouze pamatují prvních několik číslic a kolik číslic tam celkem je (exponent), velká čísla jsou typicky psána jako řekněme 3.174293⋅10¹⁹. Například typický vědecký kalkulátor ukazuje deset číslic, ale pro jistotu si jich pamatuje dvanáct. Teď si představte, co se stane, když zkusíte přičíst 20 k číslu 123456789123456789. Protože si moje kalkulačka pamatuje jen počet číslic a pak prvních dvanáct, vidí toto velké číslo jako 123456789123******. Pokud přičtete 20, ztratí se to v té části *** a kalkulačka si to nové číslo zase pamatuje jako 123456789123******. Jinými slovy, pokud přičtete takto malé číslo, vaší kalkulačce na tom nezáleží. Že se pak dostávají špatné výsledky, je nabíledni. Například následující výpočet má evidentně vyjít dvacet, ale my si ukážeme, jak to vidí má kalkulačka.

(123456789123456789 + 20) − 123456789123456789 = (123456789123****** + 20) − 123456789123****** = 123456789123****** − 123456789123******= 0.

Přesně tohle se děje v naší posloupnosti. Všimněte si, že v prvním členu máme n⁸ plus něco, a odmocnina z toho všeho. Kdyby tam nebylo to něco, odmocnina by se zkrátila s osmou mocninou a dostali bychom n⁴. To by se pak zkrátilo s "− n⁴" a posloupnost by vycházelo nulová. Hodnoty posloupnosti jsou tedy v podstatě dány tím "+ n⁵" pod odmocninou. Co se stane, když zkusíme dosadit do posloupnosti n = 10,000 = 10⁴ na mé kalkulačce? Umocníme to na osmou a dostaneme 10³², číslo s 32 + 1 = 33 číslicemi. Pak k tomu přičteme (10⁴)⁵ = 10²⁰. Tohle číslo ale ovlivní pouze pozici 20 + 1 = 21 v onom velkém čísle, neboli vůbec to nedosáhne na prvních dvanáct číslic pamatovaných kalkulačkou. Ta si tak vůbec nevšimne, že jsme to n⁵ přičetli, díky čemuž dostaneme nakonec nulu.

Teď možná řeknete, že to je sice pěkné, ale kdybyste měli kalkulačku, která si pamatuje 15 číslic, tak se to nestane. Na to říkám ano, nestane, ale jen pro n = 10,000. Pokud zkusíte n = 1,000,000, rozdíl mezi velkým a malým číslem se zvětší a ani ta lepší kalkulačka si nevšimne přičtení. Stejně lze ukázat, že ať už je váš počítač sebelepší, pokud si pamatuje jen části čísel (což u reálných čísel dělají všechny), tak nakonec - pro dost velká n - přehlédnou to přičítání. Pokud vás to zajímá, zkuste si zopakovat tu předchozí analýzu a ukažte následující: Jestliže je k přirozené číslo takové, že so počítač pamatuje nanejvýš 3k číslic reálných čísel, pak n = 10^k už stačí na jeho oblbnutí. Jinými slovy, n = 1,000,000 = 10⁶ by zmátlo počítač, který si pamatuje 18 číslic.

Dá se tomu nějak vyhnout? Existují programy, které jsou opravdu chytré a používají i algebru (například mohou znát ten trik se zbavením se odmocnin), Maple ani Matematica se tímto příkladem nenechaly zmást (ale asi by selhaly s nějakým méně zjevným). Dalším způsobem, jak vidět, co tato posloupnost dělá, je použít nějakou teoretickou znalost. Dokážu například říct - i s mou mizernou kalkulačkou - kolik vyjde a_{1,000,000,000}. Jak? Z našich intuitivních výpočtů vyplývá, že vlastně

Je to vidět takto:

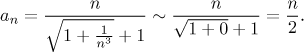
zde dokonce můžeme dostat přesnější tvrzení. Je snadné se přesvědčit, že následující nerovnosti jsou pravdivé:

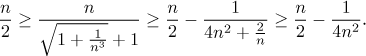
To ukazuje, že aproximace je velmi přesná, protože máme

neboli chyba aproximace je maximálně 1/(4n²), což je velmi malé číslo. (Aproximaci a_n lze také získat pomocí Taylorova polynomu.) Když toto srovnáte s hodnotami v tabulce nahoře, uvidíte, že se dobře shodují až po n = 1000, než se kalkulačka ztratila. Pomocí této aproximace teď hravě spočítáme, že a_{1,000,000,000} ∼ 500,000,000±1, ani jsme na to nepotřebovali tu kalkulačku. Pro takto velká n je aproximace extrémně přesná, maximální možná chyba teď je 0.0000000000000000025.

Celou tuto stať byste měli brát hlavně jako varování. Pokud poštvete svou kalkulačku na danou posloupnost, odpovědi, které naznačí, mohou být zcela mimo. Nicméně pro většinu posloupností dostanete dobré typy, takže když na nějaký problém nemůžeme teoreticky, často se snažíme získat lepší pohled pomocí počítačů. V příští sekci uvidíte pár zajímavých příkladů, kdy počítače pomůžou.

Pí a Eulerovo číslo
Zpět na Teorie - Aplikace