Příklad: Najděte (pokud existují) limity funkce

v x = 0 a v nekonečnu.

Řešení:
Limita v x = 0.
Je to standardní problém, máme najít limitu výrazu, který existuje na prstencovém okolí limitního bodu. Tohle vlastně není až tak jasné, takže začneme tím, že si daný výraz přepíšeme do správného tvaru, protože obecné mocniny máme zkoumat ve tvaru "e na ln".

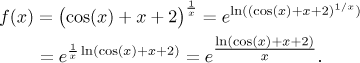
Když je x blízko 0, například jestliže |x| < 1, pak je kosinus přinejmenším 0, takže dostaneme cos(x) + x + 2 > 1. Logaritmus proto existuje a tedy i celý daný výraz existuje na prstencovém okolí nuly (−1,0) ∪ (0,1).

Toto potvrzuje, že otázka má smysl, a můžeme začít obvyklým způsobem, tedy dosadíme 0 do výrazu. Protože budeme pracovat s funkcí ve tvaru "e na ln" a exponenciálu je možné vytáhnout z limity, na chvíli se soustředíme jen na výraz uvnitř exponenciály.

Dělení nenulového čísla nulou je neurčitý výraz, pokud tedy nepřinutíme nulu ve jmenovateli, aby byla jednostranná. Pro to ale nevidíme žádný důvod, což vzbuzuje podezření, možná limita ani neexistuje. Abychom to věděli najisto, použijeme standardní trik a podíváme se na jednostranné limity:

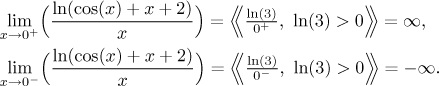
Protože jednostranné limity nesouhlasí, daná (oboustranná) limita neexistuje. Poznamenejme, že bylo nutno se zamyslet nad hodnotou čísla ln(3), protože kdyby bylo ln(3) záporné, pak by ta nekonečna byla naopak, a pokud by to byla nula, pak bychom dostali neurčitý podíl a byl by třeba jiný přístup k problému.

Teď bychom rádi prohlásili, že když umocňujeme e na výraz, který nemá limitu, pak dostaneme něco, co také nemá limitu. V tomto případě je to dokonce pravda, ale není to hned zjevné a nejde o pravidlo, které by platilo pro všechny funkce (neplatí dokonce ani pro všechny pěkné funkce). Abychom to tedy hráli na jistotu a ukázali pořádné řešení, podíváme se na jednostranné limity samotné funkce f, samozřejmě využijeme již provedené výpočty.

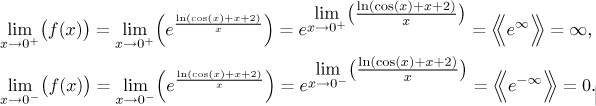
Toto potvrzuje, že limita f v x = 0 neexistuje.

Limita v nekonečnu.
Z nerovnosti cos(x) + x + 2 > x vidíme, že logaritmus ve zkoumaném výrazu existuje pro všechna kladná x, funkce je tedy definovaná na okolí nekonečna a má smysl tam hledat limitu. Jako obvykle začneme dosazením nekonečna do daného výrazu.

Je to neurčitý výraz? To není hned jasné. Dá se ukázat, že čitatel opravdu utíká do nekonečna (viz níže), ale my to vlastně nepotřebujeme, protože máme tu nádhernou obecnější verzi l'Hospitalova pravidla, která nám teď ušetří čas.

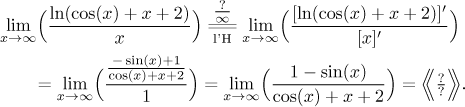
Co můžeme říct o výrazech ve zlomku? V čitateli máme oscilující, ale omezený výraz, který neustále osciluje mezi 0 a 2. Ve jmenovateli se kosinus coby omezená funkce přičítá k výrazu "x + 2", který jde v nekonečnu do nekonečna. To by mělo připomenout pravidlo "omezená plus nekonečno je nekonečno". Abychom to měli na jistotu, tak toto dokážeme, nejjednodušší se zdá být srovnávací test. Pro x > 0 opravdu máme

cos(x) + x + 2 ≥ (-1) + x + 2 = x + 1→∞ v nekonečnu.

Toto potvrzuje, že výraz ve jmenovateli jde do nekonečna, teď bychom mohli použít pravidlo "omezená děleno nekonečnem je nula". Pro úplnost to zase dokážeme, tentokráte bude třeba oboustranné srovnání neboli Věta o sevření:

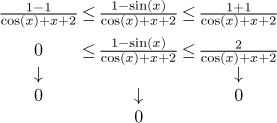
Potvrdili jsme, že výraz jde v nekonečnu k nule. Teď si ale musíme vzpomenout, že nám nejde o tento konkrétní výraz, ale o "e na tento výraz". Musíme se tedy vrátit k dané funkci.

Další příklad
Zpět na Řešené příklady - Limita