Here we will explore closer some interesting situations with oscillation. It is assumed that the reader already checked on the previous problem. We will skip complete and formal proofs as we prefer to develop intuition here. Formal proofs would be similar to those in the previous problem, either proving in the positive using comparison or disproving using Heine's theorem.

Problem: Evaluate (if it exists)

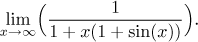
Solution: We already investigated the behaviour of the expression x(1 + sin(x)) in the previous problem, so we know that it oscillates between 0 and 2x as we approach infinity with x. It is also always positive or zero, so 1 + x(1 + sin(x)) is at least 1 and oscillates between 1 and 1 + 2x. Consequently, when we put it into a denominator of a fraction with 1 on the top, this fraction will oscillate between 1 and 1/(1 + 2x). Since the latter tends to zero at infinity, for really large values of x the given expression oscillates between 1 and "almost 0", our guess therefore is that the limit does not exist. To prove it we would consider sequences x_n = π/2 + 2nπ and y_n = 3π/2 + 2nπ. The situation looks roughly like this:

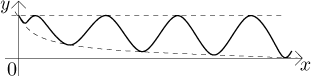
Note: We had to put "1 +" in the denominator, since the expression x(1 + sin(x)) is zero at infinitely many points going to infinity. Therefore there is no neighborhood of infinity where the resulting fraction would exist, hence limit there would not make sense. This is not a problem in the following expression.

Problem: Evaluate (if it exists)

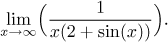
Solution: The sine oscillates between −1 and 1, so 2 + sin(x) oscillates between 1 and 3 included. Thus x(2 + sin(x)) oscillates between x and 3x, in particular it goes to infinity. Consequently, 1 over this expression goes to zero. How would we prove it? If an expression with a bounded oscillation goes to zero, the absolute value version of the Squeeze theorem seems best. At infinity we have

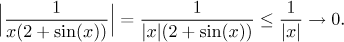
By the way, once we understand how 2 + sin(x) behaves, we can easily guess that

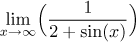
does not exists (the fraction oscillates between 1 and 1/3) and that

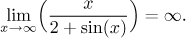
Here we would use one-sided comparison, we can estimate the given expression from below by x/3 to push it up.

Problem: Evaluate (if it exists)

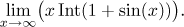
Solution: The expression 1 + sin(x) oscillates between 0 and 2 included, so when we apply the function integer part to it, we will get constant parts with values 0, 1 and 2.

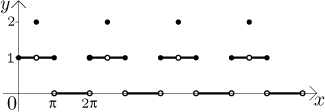
When we multiply this by x, we get oblique segments that lie on the lines y = 0, y = x, and y = 2x.

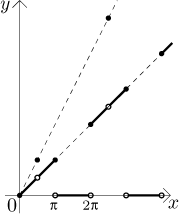
Thus the limit does not exist.

By the way, what can we say about the expression Int(0.9 + 0.9sin(x))? The expression 0.9 + 0.9sin(x) oscillates between 0 and 1.8 included, so when we apply the integer part to it, we get segments at levels 0 and 1. Thus there are two differences compared to the previous example. The first difference is that the expression has only two values, we got rid of the one-point dots at level 2 above that might cause troubles. One possible application is to use this in the expression

1/2 − Int(0.9 + 0.9sin(x)),

which now has two distinct values, −1/2 and 1/2.

The second difference is that now the segments at level 0 are longer than the segments at level 1, unlike the previous example, where the picture was nicely regular.

Finally, the expression x⋅Int(0.9 + 0.9sin(x)) gives segments that lie in turn on the line y = x and y = 0.

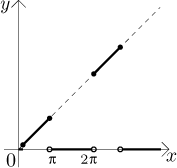
Thus the limit of this expression at infinity does not exist.

Problem: Evaluate (if it exists)

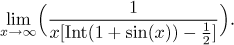
Solution: We know that Int(1 + sin(x)) is a function that consists of segments at levels 0, 1, and 2 (there are just dots there). When we subtract 1/2, we get a function whose graph is segments at levels −1/2, 1/2, and 3/2. Thus the function x[Int(1 + sin(x)) − 1/2] has a graph that consists of segments that lie on lines y = −x/2, y = x/2, and y = 3x/2.

Since the graph keeps jumping between lines that go to infinity and a line that goes to negative infinity, it follows that it does not have any limit at infinity. What do we get when we divide 1 by this expression? The given expression is sometimes equal to −2/x, sometimes 2/x and sometimes 2/(3x). All three curves tend to zero at infinity, so any function that jumps between these three graphs also has to tend to zero.

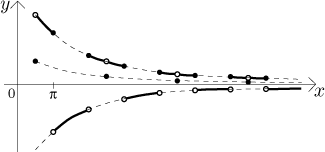
How would we prove it? Since we have an oscillating expression with bounded parts, we would guess that comparison can help. Since we want to prove that something goes to zero, the absolute value version of the Squeeze theorem seems best.

Next problem
Back to Solved Problems - Limits