Problem: Evaluate (if it exists) the limit

Solution: This is a standard problem, we want to find a limit at infinity of an expression that exists on a neighborhood of infinity (e.g. for x > 0). Thus we start by substituting infinity into the expression.

where N stands for a limit that does not exist. We can try to call on the algebra of N, but it does not help us anyway, since it says that ∞⋅N is an indeterminate expression. We know that sine is a bounded function, but bounded times infinity can be anything, so this is no use. What do we do? One possibility is to use the l'Hospital rule, since it has not only the indeterminate ratio version, but also a more general "something over infinity" version.

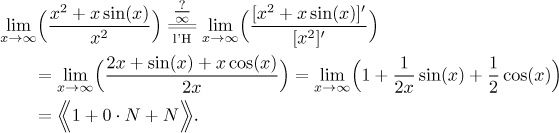
Again we have an expression that cannot be handled using the limit algebra and the algebra of N. However, this time we get some help from boundedness, since there si a rule "bounded times zero is zero". Thus we get

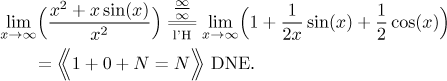
Thus the limit that we obtained after the l'Hospital does not exist, which is rather bad; the l'Hospital rule states that the equality is valid only if the limit on the right exists. Here it does not, so the l'Hospital step was not justified and the given limit can be just anything. Obviously we need a different approach.

This problem does not exactly fit some standard box, but it is related somehow to the box "polynomials at infinity" and above all to the box "comparison and oscillation". When facing a non-typical problem, it is usually helpful to get some feeling for the behaviour of the given expression, which is where the intuitive evaluation comes in. What happens when x grows large?

The sine oscillates between −1 and 1, so the term x⋅sin(x) oscillates between the values x and -x, that is, its limit at infinity does not exist. It is added to the term x², how do they compare? The oscillating term is never larger (in absolute value) than x, so around infinity it is insignificant compared to x². Thus we get

How do we prove such a guess? The intuitive evaluation approach calls for factoring out dominant terms. Here they are the same in the numerator and the denominator, so it is faster to just divide both parts by x².

How did we know that the second term goes to zero? We used the rule "zero times bounded is zero". What if this rule was not covered in your course, so you are not allowed to use it? Or what if you do not trust it? A complete proof can be done using methods from the box "comparison and oscillation". We have an oscillating part in the given expression and this part is bounded, so it fits quite well. We claim that there is a proper limit, such claims are usually done using the Squeeze theorem. We will show in detail how one can derive an estimate for the given expression using a known bound and algebra. Since we are interested in limit at infinity, we will do our estimates for x large, in particular for x > 0 (we will need this).

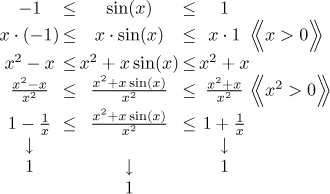
This concludes the problem, we proved that the given expression goes to 1 at infinity.

Remark: To get a better feeling for this behaviour, we will look at some modifications of this problem.

Problem:

The numerator is the same as above, so it behaves like x², but this time the denominator is only x, so the fraction should go to infinity. Again, we can prove it by comparison, but since here we have an improper limit, we can try one-sided comparison since it is easier. We will need a lower estimate to push the given expression up.

Problem:

Now we have a different situation in the numerator. As we observed above, the product x⋅sin(x) oscillates between -x and x, so when we add x, we get something that oscillates between 0 and 2x. Then we divide by x, so the fraction should oscillate between 0 and 2 as we go to infinity, that is, our guess is that the limit does not exist. How do we confirm it?

One possibility that works here is to divide and use the algebra of N.

However, since this algebra is usually not covered, we need a different solution that would satisfy everybody. In the case of oscillation one would typically use the Heine theorem. In order to prove that no limit exists we will construct two sequences, {x_n} and {y_n}, that go to infinity, but when we substitute them into the given expresssion, we get different limits. Obviously, we wil use the first sequence to hit "hills" in the oscillating wave, the second one usually hits "dips", but here it might be easier to go for the "midway" points.

First, define x_n = π/2 + 2nπ. Then x_n→∞. When we substitute it into the given expression f (x), we get f (x_n) = 2→2.

Next we define y_n = nπ. Again y_n→∞. When we substitute it into the given expression f (x), we get f ( y_n) = 1→1.

This proves that f cannot have a limit at infinity, since this limit would have to be equal to both 2 and 1, a contradiction.

Problem:

Now the numerator is the same as in the previous example, so it oscillates between 0 and 2x. When divided by x², the whole fraction should go to zero at infinity. If we can rely on the "zero times bounded is zero" rule, we can calculate like this:

If a more complete proof is needed, the easiest way out is the absolute value version of the Squeeze theorem.

Next problem
Back to Solved Problems - Limits