Zde nebudeme chápat asymptoty jako teoretické srovnání funkcí okolo bodů (viz Řád funkce a asymptoty v části Funkce - Teorie - Reálné funkce). Pro účely kreslení grafů je budeme brát jako přímky, které mají tu vlastnost, že je následují některé "konce" grafu. To volá po jiné definici; takové máme dvě nebo tři (podle toho, jak je počítáme).
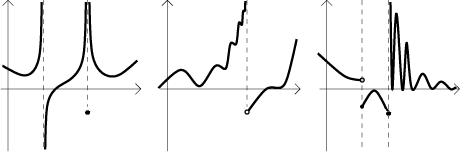
Svislé asymptoty. Než uvedeme formální definici, podíváme se na tento obrázek:

První dva obrázky vlevo ukazují svislé asymptoty, svislé přímky v posledním obrázku napravo asymptoty nejsou (situace napravo v obrázku je taková, že funkce neustále osciluje nahoru a dolů, jak se k tomu bodu blíží, a velikost oscilace roste do nekonečna, pro podobný příklad viz Příklad 3 v sekci "pilovité" funkce v části Funkce - Teorie - Elementární funkce). To by mělo naznačit správnou definici.
Definice.
Řekneme, že funkce f má svislou asymptotu v a (nebo že přímkax = a je svislá asymptota f ) jestliže alespoň jedna jednostranná limita f v a je nevlastní.
Tato definice nám také říká, jak takovou asymptotu najít. Nejprve shromáždíme všechny kandidáty. Z definice je jasné, že pokud je f spojitá v a, pak tam nemůže mít svislou asymptotu. Co zůstalo? Vlastní koncové body intervalů, ze kterých se skládá definiční obor, a body uvnitř těchto intervalů, kde f není (nebo by nemusela být) spojitá. Pro každý z těchto bodů se podíváme na všechny možné jednostranné limity a pokud je alespoň jedna nevlastní, dostaneme tam svislou asymptotu.
Jako obvykle se nic špatného nestane, pokud přidáme do našeho seznamu kandidátů body navíc, jednoduše je v dalším kroku vyřadíme. To je také důvod, proč se v praxi nenamáháme opravdu hledat body nespojitosti, prostě mezi kandidáty zahrneme všechny body, kde to se spojitostí vypadá podezřele. Jednostranné limity pak rozhodou o asymptotách, poznamenejme, že kdybychom opravdu chtěli znát spojitost v těchto bodech, tak bychom stejně museli tyto jednostranné limity počítat, takže tím, že do ní tolik nevrtáme, ušetříme čas. Další čas ušetříme, pokud je v daném bodě už první jednostranná limita nevlastní, pak už totiž asymptotu máme a není důvod počítat tu druhou (pokud nějaká je).
Vodorovné asymptoty. Než uvedeme formální definici, podíváme se na tento obrázek:
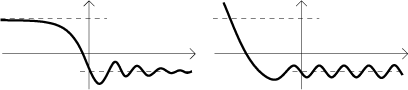
První obrázek ukazuje vodorovné asymptoty, vodorovné přímky v druhém obrázku asymptoty nejsou. To naznačuje, jak má vypadat správná definice.
Definice.
Nechť je funkce f definovaná na okolí nekonečna. Řekneme, že přímkay = a je vodorovná asymptota funkce f v nekonečnu, jestliže limita f v nekonečnu je a.
Nechť je funkce f definovaná na okolí mínus nekonečna. Řekneme, že přímkay = a je vodorovná asymptota funkce f v mínus nekonečnu, jestliže limita f v mínus nekonečnu je a.
Tato definice nám rovnou říká, jak takové asymptoty hledat.
Šikmé asymptoty. Než uvedeme formální definici, podíváme se na obrázek:
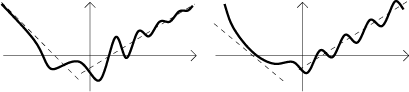
První obrázek ukazuje šikmé asymptoty, přímky v druhém obrázku asymptoty nejsou.
Definice.
Nechť je funkce f definovaná na okolí nekonečna. Řekneme, že přímkay = Ax + B je šikmá asymptota funkce f v nekonečnu, jestliže
Nechť je funkce f definovaná na okolí mínus nekonečna. Řekneme, že přímka
y = Ax + B je šikmá asymptota funkce f v mínus nekonečnu, jestliže
Jak takové asymptoty hledáme?
Fakt.
Nechť je funkce f definovaná na okolí nekonečna. Přímkay = Ax + B je šikmou asymptotou f v nekonečnu tehdy a jen tehdy, když
Odpovídající tvrzení platí i pro asymptoty v mínus nekonečnu. Vidíme, že abychom dostali přímku, musí konstanty A a B existovat, jinými slovy ony dvě limity by měly konvergovat. Pokud konvergují, dostaneme asymptotu. Poznamenejme také, že k výpočtu druhé limity potřebujeme znát výsledek první. To naznačuje, jak obecně postupovat při hledání šikmých asymptot.
Začneme první limitou. Pokud diverguje, pak v nekonečnu není asymptota.
Jestliže konverguje, můžeme zkusit druhou limitu. Pokud tato diverguje, není
v nekonečnu žádná asymptota. Pokud konverguje, máme tam asymptotu
Poznámka: Všimněte si, že tento postup také dává vodorovné
asymptoty. Jestliže totiž má f limitu b v nekonečnu, pak tento
postup nejprve dá
Jsou na to docela dobré důvody. Vodorovná asymptota se liší ve dvou důležitých aspektech. Za prvé, je mnohem snažší ji najít než nevodorovné šikmé asymptoty, prostě jen interpretujeme limitu v (mínus) nekonečnu. Za druhé, když má funkce vodorovnou asymptotu v nekonečnu, je její chování velmi rozdílné od funkcí, které tam mají nevodorovné šikmé asymptoty. Přesto někteří autoři nepovažují tyto důvody za dostatečně důležité, aby jeden pojem rozdělili na dva, prostě jen pracují se svislými a šikmými asymptotami.
Zde v Math Tutoru ale vodorovné asymptoty bereme jako speciální případ, což nám také umožňuje dále zpřesnit algoritmus pro šikmé asymptoty. Vždy začneme s limitou v nekonečnu (pro mínus nekonečno máme evidentní modifikaci). Jestliže limita neexistuje, pak tam není vůbec žádná asymptota. Pokud je vlastní, pak tam máme vodorovnou asymptotu. Pokud je nevlastní, pak je šance na šikmou asymptotu.
Zkusíme pak příslušnou limitou najít A. Jestliže diverguje, pak tam
nemáme šikmou asymptotu. Teď ale i výsledek
Pro praktický přehled odkazujeme na sekci Asymptoty v části Přehled metod - Průběh funkce.
Příklad: Najděte všechny asymptoty funkce
![]()
Řešení:
Definiční obor je
![]()
Dostali jsme nevlastní jednostrannou limitu, takže už není nutné dívat se na
tu druhou. Víme, že f má svislou asymptotu v
Teď se podíváme na nekonečno:
![]()
Není tedy vodorovná asymptota, ale může být šikmá. Zkusíme najít A:
![]()
Takže v nekonečnu nemáme ani šikmou asymptotu.
Teď se podíváme na mínus nekonečno:
![]()
Máme vodorovnou asymptotu