Příklad: Najděte definiční obor a limity v krajních bodech jeho intervalů funkce
![]()
Řešení: Tato funkce je obecná mocnina, takže abychom ji mohli zkoumat, musíme ji nejprve přepsat do kanonického tvaru.
![]()
Teď se podíváme, které podmínky určují definiční obor. Exponenciála spolkne cokoliv, ale v jejím exponentu máme logaritmus a ten vyžaduje, aby byl zlomek uvnitř kladný. Máme i druhou podmínku, zlomek očekává nenulový jmenovatel. Podíváme se blíže na první podmínku. Zlomek má být větší než nula, což je znaménková nerovnost a můžeme ji vyřešit tak, že uvažujeme oblasti různých znamének. Dělící body jsou −1 a 1, dostaneme

Definiční obor je tedy dán vnějšími intervaly, ostrá nerovnost znamená, že mají být otevřené, což rovnou vyřeší i podmínku pocházející ze zlomku (ve jmenovateli nebude nula).
Máme čtyři limity k výpočtu. Vezmeme to zleva, pro rady o počítání limit viz např. Limita v části Funkce - Přehled metod.
![]()
Abychom ušetřili čas a místo, vynecháme v dalších výpočtech tu exponenciálu, ale musíme si pamatovat ji zase na konci vrátit. Nejprve musíme zjistit, so dělá zlomek uvnitř logaritmu. To je vlastně velice snadné, pro podíl dvou polynomů můžeme použít trik s vytknutím vedoucích mocnin, zde je dokonce můžeme vykrátit, protože jsou stejné.
![]()
Máme neurčitý součin a použijeme příslušný trik.
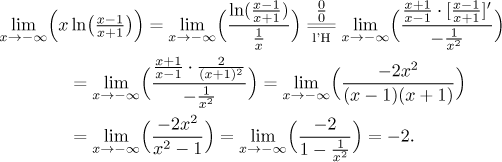
Teď si musíme vzpomenout na tu exponenciálu.
![]()
Nyní se podíváme na limitu v −1 zleva, začneme bez exponenciály.
![]()
Proto
![]()
Limita v 1 zprava je podobná.
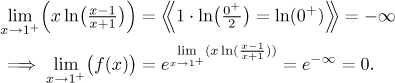
Nakonec se dostáváme k limitě v nekonečnu, zde jsou výpočty analogické těm pro mínus nekonečno.
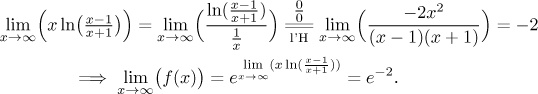
Zase můžeme zkusit výsledky vyjádřit pomocí náčrtku. Z kanonického tvaru také vidíme, že f je vždy kladné, a tak se v našem obrázku nemusíme zabývat zápornými hodnotami.
