"Related rates": Přehled metod

Problém: Máme dvě kvantity, f a g, obě závisí na čase. Chceme najít nějaký vztah mezi jejich derivacemi podle t.

Řešení:
Krok 1. Najdeme nějaký vztah mezi f a g, obvykle ve tvaru f = F(g).
Krok 2. Tento vztah zderivujeme, na pravé straně pomocí řetízkového pravidla.

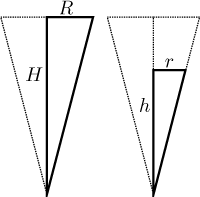
Příklad: Číška na víno má tvar pravidelného kužele o výšce 8 cm a poloměru podstavy 2 cm. Začneme ji plnit vínem rychlostí 4 cm³ za sekundu. Jak rychle stoupá hladina vína v okamžiku, kdy je sklenice napůl plná?

Řešení: Máme dvě kvantity, které se mění, objem vína ve sklenici V a výška hladiny h. Kužel má parametry H = 8 a R = 2. Rychlost změny, kterou máme zadánu, můžeme vyjádřit pomocí právě zavedených proměnných jako V ′(t) = 4.

Chceme vědět rychlost změny h. Na to nejprve potřebujeme nějaký vztah mezi V a h, ale objem závisí na výšce a poloměru. Abychom spočítali poloměr v závislosti na výšce, použijeme podobnost trojúhelníků.

Odtud víme, že r:h = R:H, proto r = h/4. Teď snadno spočítáme objem v závislosti na h:

Zderivujeme obě strany podle t, přičemž pamatujeme, že r je také funkce t. Použijeme Leibnizovo značení, protože se na tohle zdá se hodí lépe.

Odtud dostaneme

Máme výraz pro rychlost změny výšky hladiny vína, zbývá dosadit dané údaje, mimo jiné máme h = H/2 = 4. Odpověď tedy je, že když je sklenice z poloviny plná, stoupá hladina rychlostí 4/π cm/sec.

Pro hlubší pohled na téma a další příklad viz "Related rates" v části Teorie - Aplikace, viz také Řešené příklady - Aplikace.

Globální extrémy, optimalizace
Zpět na Přehled metod - Aplikace