Příklad: Vypočítejte integrál
![]()
Řešení: Ten "extra kosinus" vedle dx přímo volá po sinové substituci.
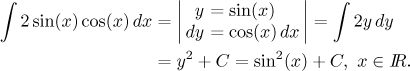
Je tam ovšem také "extra sinus", takže si sami ověřte, že substitucí
![]()
Některým čtenářům přišel určitě výraz v integrálu povědomý. To je třetí možné řešení, integrál nejprve upravit pomocí goniometrické identity a pak pokračovat substitucí.
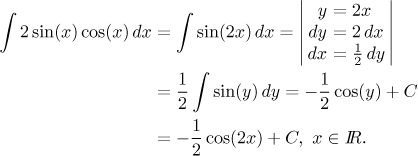
Zdá se, že jsme dostali tři různé výsledky, protože rozhodně není pravdivá ani jedna z následujících rovností:
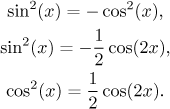
Tajemství je skryto v magické kostantě +C, která reprezentuje
libovolné číslo. Nikde není řečeno, že to číslo musí být ve šech výsledcích
stejné, čili vlastně bychom u každého výpočtu měli použít jiné písmenko -
právě v té různosti je schována rovnost integrálů. Výše uvedené výrazy se
totiž sice liší, ale liší se vždy o konstantu, jsou tedy všechny primitivními
funkcemi k
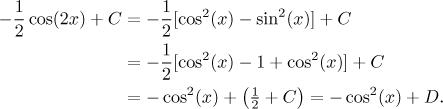
Ponaučení tedy je, že pokud se výsledek našeho výpočtu liší od jiného výsledku k témuž příkladu, je to v pořádku, pokud se liší pouze o konstantu. Pokud si nejste jisti, udělejte zkoušku.
Při hledání řešení jsme se nechali řídit intuicí. Kdybychom na to chtěli jít podle šuplíků, tak bychom se museli zeptat šuplíku goniometrické integrály a dostali bychom rady, které vedou na ty tři metody výše.
Tento integrál lze vyřešit ještě dvěma dalšími způsoby, jmenovitě pomocí integrace per partes. Hodí se to k tomuto typu? Je to součin a jednu část umíme snadno integrovat. Druhá část by se měla derivováním zlepšit, tak to zde neplatí, takže to není zrovna nejlepší per partesí kandidát. Nicméně zkusme se nechat překvapit.
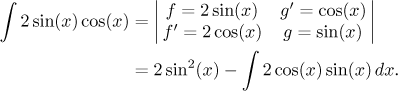
Skončili jsme překvapivě se stejným integrálem, což není na závadu, převedeme jej na levou stranu a dostaneme rovnici. Zde je nutné si uvědomit, že primitivní funkce na pravé straně se od těch nalevo mohou lišit o konstantu, proto napravo po odečtení neznámá konstanta zbude.
![]()
No teda, to je přesně ten první výsledek. Mimochodem, byl nějaký důvod k
tomu, abychom vzali jako f ten sinus? Popravdě řečeno ne, prostě jsme
to brali odleva. Klidně se dá jako f vzít kosinus a jako
Tento příklad lze tedy řešit přinejmenším pěti různými způsoby. Trochu mě mrzí, že z per partes nevypadnou další možné výsledky a že nelze aplikovat parciální zlomky, to bychom na tomto příkladě ukázali všechny základní metody. Ale i tak je pěkný.