Aproximace řad: Přehled metod

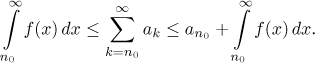
Zde se podíváme na dvě témata.

1. Teoretický odhad součtu dané řady.

Zde je hlavním nástrojem integrální kritérium, viz Teorie - Testování konvergence. Jestliže členy a_k dané řady pochází z nějaké kladné a nerostoucí funkce f jako a_k = f (k), pak můžeme součet naší řady odhadnout:

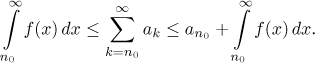
Pro příklad se podívejte na Integrální kritérium v části Teorie - Testování konvergence.

2. Odhad chyby při aproximaci řady konečným součtem.

To se dá často udělat aplikací předchozího odhadu na konec řady. V kombinaci se srovnáním (viz Srovnávací kritéria v části Teorie - Testování konvergence) dostaneme obecnější tvrzení.

Uvažujme konvergentní řadu  a_k  reálných čísel.
• Jestliže existuje řada  ∑ b_k  reálných čísel a celé číslo N takové, že |a_k| ≤ b_k pro k > N, pak

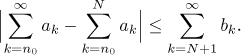
• Jestliže existuje kladná nerostoucí funkce g a celé číslo N takové, že |a_k| ≤ g(k) pro k > N, pak

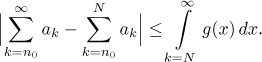
Příklad: Chceme aproximovat součet řady 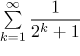   pomocí jejího částečného součtu s přesností 0.0001.

Jaká je chyba aproximace součtu řady pomocí jeho prvních N členů? Pomocí prvního přístupu se zbavíme té nepříjemné části "+1".

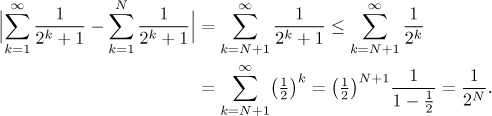
Teď už jen najdeme N tak, aby výsledný odhad chyby byl nanejvýš 0.00001, takže odpověď je, že N = 17 stačí. Sečteme tedy prvních 17 členů dané řady a už známe její součet s danou přesností.

Pro příklad použití druhého přístupu přes funkce se podívejte na příklad v sekci Integrální kritérium v části Teorie - Úvod a tento příklad v části Řešené příklady - Sčítání řad.

Obecně můžeme zkusit odhadnout chybovou řadu shora (v absolutní hodnotě) libovolnou jinou konvergentní řadou, jejíž součet jsme schopni určit, často to znamená geometrickou řadu. Viz tento příklad v části Řešené příklady - Sčítání řad.

Máme také odhad pro alternující řady.

Uvažujme řadu  a_k  reálných čísel. Předpokládejme, že a_k = (−1)^kb_k pro nějakou nerostoucí posloupnost {b_k} kladných čísel jdoucích k nule. Pak

Pro příklad viz tento příklad v části Řešené příklady - Sčítání řad.

Zpět na Přehled metod - Sčítání řad