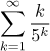
Příklad: Aproximujte součet řady

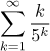
pomocí jejího částečného součtu s₂₀ a odhadněte chybu této aproximace.

Řešení: Snadno se ukáže pomocí například podílového kritéria nebo odmocninového kritéria, že daná řada konverguje (prakticky identický příklad lze nalézt v sekci Odmocninové a podílové kritérium v části Teorie - Testování konvergence), takže otázka má smysl.

Moje kalkulačka říká, že

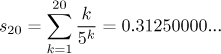
Chyba aproximace je

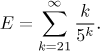
K odhadu zbytku řady se hned nabízí použít integrální kritérium. Pomocí derivace snadno dokážeme, že funkce f (x) = x⋅5^−x je klesající na intervalu ⟨21,∞), je tam také kladná, takže se dá integrální kritérium aplikovat. Pomocí integrace per partes a l'Hôpitalova pravidla dostaneme

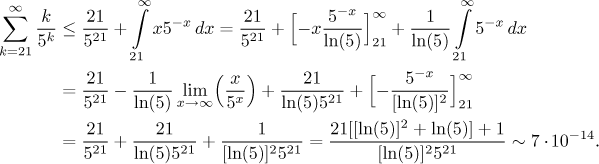
Máme tedy

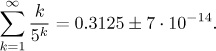
Alternativa: Onen odhad pomocí integrálu výše je velice citlivý, i malá změna v řadě vyrobí funkci, u které nebudeme moci doufat, že ji zintegrujeme. Obecně proto děláme něco jiného: Hledáme horní odhad dané řady řadou jinou, která by byla podobná, konvergentní a kterou bychom nějak dokázali sečíst či její součet snadno odhadnout (například i pomocí integrálu). Jaký odhad můžeme použít pro naši danou řadu?

U typické řady jsou často ve členech části, které lze pro velké hodnoty k ignorovat (viz intuitivní výpočet v části Posloupnosti - Teorie - Limita), to nám pak napoví při hledání dobrého horního odhadu. Zde tomu tak ale není, takže to bude chtít více tvůrčí přístup. Jednu řadu známe dobře, jmenovitě geometrickou řadu. Abychom dostali odhad dané řady shora pomocí geometrické řady, potřebovali bychom takový odhad pro k. Ale protože výrazy q^k rostou rychleji než k pro q > 1, tak by to neměl být problém. Je jasné, že se budeme snažit udělat q co nejmenší, rozhodně budeme potřebovat, aby bylo menší než 2, protože výsledná řada bude mít v sobě q/2.

Tak například pro k > 20 máme k < (1.5)^k. Jak si můžeme být jisti? Použijeme metodu uvedenou v sekci Použití derivace k porovnávání funkcí v části Derivace - Přehled metod. Označme f (x) = x a g(x) = (1.5)^x. Pak f (20) < g(20) a f ′(x) < g′(x) pro všechna x > 20, což dokazuje naše tvrzení.

Jsme tedy oprávněni odhadovat

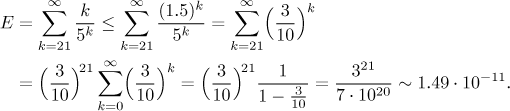
Je to o něco horší než ten předchozí odhad, ale není to tak špatné a na rozdíl od té metody výše, která je tak citlivá na integraci, tahle má dobrou šanci uspět, když vám někdo prostě předhodí řadu. Kvalita odhadu se dá vylepšit tím, že utáhneme horní mez, tedy použijeme číslo menší než 1.5. Trocha experimentování ukáže, že také k < (1.2)^k pro k > 20, takže dostaneme

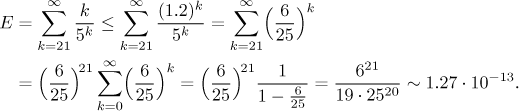
To už je skoro tak dobré, jako ten první odhad. Ověřte, že když použijete 1.17 namísto 1.2, tak ten odhad chyby stáhnete na 7.40⋅10⁻¹⁴, což už je téměř dokonalé. Jestli chcete, můžete si ještě pohrát, ale protože náš první odhad byl velice těsný, tak už nemůžete doufat v nic víc, než že se od 7.4 posunete k 7, ten řád už je to nejlepší, co lze dostat. Mimochodem, jak malé číslo je možné použít? Důkaz nerovnosti s derivací, který jsme použili výše, ukazuje, že a^k je horním odhadem pro k (pro k > 20), jestliže 20 ≤ a²⁰ a 1 ≤ ln(a)⋅a²⁰. Použijeme-li tu první podmínku, tak lze tu druhou nahradit vztahem jednodušším, ln(a) ≥ 1/20.

Další příklad
Zpět na Řešené příklady - Sčítání řad