Věta (srovnávací kritérium).
Uvažujme řady
• Jestliže
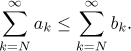
• Jestliže
V předchozí sekci jsme se snažili porovnávat řady s geometrickou řadou. Existuje ještě jeden typ řady, kterému dobře rozumíme, jmenovitě p-řada (řada s mocninami). Když je nám dána řada, můžeme se zeptat, jestli není podobná nějaké p-řadě; obecněji, zkoušíme ji porovnat s nějakou jinou řadou, kterou dobře známe. Hlavní trik používaný v takových porovnáních je ingorování částí, které jsou pro velká k méně důležité (viz např. Intuitivná výpočet v čísti Posloupnosti - Teorie - Limita).
Jestliže chceme dokázat, že chování dané řady je podobné jako chování jiné (asi jednodušší) řady (budeme jí říkat testovací řada), máme dvě možnosti. Jedna je přímé porovnání.
Věta (srovnávací kritérium).
Uvažujme řady∑ ak a∑ bk splňující0 ≤ ak ≤ bk pro všechna k.
• Jestliže∑ bk konverguje, pak také∑ ak konverguje a
• Jestliže
∑ ak diverguje, pak také∑ bk diverguje.
Hlavní myšlenka této věty je velice jednoduchá: Jestliže platí nějaká nerovnost mezi členy řad, pak je stejná nerovnost také pravdivá mezi řadami; jako bychom sečetli všechny jednotlivé nerovnosti, což je něco, co můžeme bezpečně dělat s konečně mnoha nerovnostmi. Tato věta ukazuje, že to také jde s nekonečně mnoha, pokud jsou čísla v nich kladná a pokud se smíříme s představou, že z toho občas nic nevyjde.
Zkuste si představit, že uděláme následující:
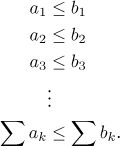
Jaký smysl má poslední řádek? Věta říká, že selský rozum nám dá správnou odpověď. Za prvé, předpokládejme, že řada nalevo diverguje. Pak je její součet nekonečno (podle této věty, její členy jsou kladné nebo nula) a suma napravo je větší, takže musí být také nekonečná. Tím jsme dostali druhé tvrzení výše.
Pokud řada nalevo konverguje, pak je součtem reálné číslo. Řada napravo je větší, ale to může znamenat větší (či stejné) reálné číslo nebo také nekonečno. Selský rozum naznačuje, že řada napravo má příliš volnosti. A opravdu, věta výše nám pro tuto situaci nenabízí žádný závěr.
Teď předpokládejme, že řada napravo konverguje. Pak je jejím součtem reálné číslo a součet nalevo je menší (či roven), takže to také musí být reálné číslo a dostaneme konvergenci. (Tohle je choulostivý moment, jak víme, že řada nezačne oscilovat v prostoru vymezeném horní mezí? Zde nás zachrání kladnost členů, bez nich by srovnání selhalo.)
A nakonec, pokud řada napravo diverguje, pak je její součet nekonečno (zase ty kladné členy) a součet nalevo je menší nebo roven. Může to tedy být reálné číslo nebo nekonečno, neumíme se rozhodnout a žádný závěr není možný.
Právě jsme viděli dobré důvody pro to, že jsou tvrzení ve větě jen implikace, nikoliv ekvivalence. To je právě hlavním problémem tohoto kritéria. Když ukážeme nerovnost mezi dvěma řadami a získáme informace o konvergenci jedné z nich, tak máme jen 50 procent šance, že se tuto informaci podaří přetáhnout ke druhé řadě. Ještě jedna poznámka: Jestliže je byť jediná z nerovností mezi jednotlivými členy ostrá, pak také nerovnost mezi řadami bude ostrá. (Čímž se nic nezmění na podstatě kritéria, i mezi dvěma nekonečny může být ostrá nerovnost.)
Příklad: Vyšetřete konvergenci
![]() .
.
Použijeme srovnávací kritérium. Nejprve musíme najít dobrou testovací řadu. Nejlepší způsob jejího nalezení je obvykle položit si otázku, které části ak nejsou pro velká k důležité. V tomto případě víme, že lze ignorovat to "+13". Tímto způsobem dostaneme testovací řadu a pokračujeme tím, že se snažíme najít nějaké porovnání mezi danou řadou a testovací řadou (obě mají kladné členy, tudíž není problém se srovnávacím kritériem).
![]()
Protože o řadě napravo víme, že konverguje (p-test, viz Důležité příklady v části Teorie - Úvod), a je větší, tak také daná řada musí konvergovat.
Příklad: Vyšetřete konvergenci
![]() .
.
Použijeme srovnávací kritérium. Už jsme viděli nejpřirozenějšího kandidáta na testovací řadu, takže to zkusíme.
![]()
Řada nalevo konverguje, ale ta napravo je větší, takže může být také nekonečná. Tentokrát srovnávací kritérium nevedlo k žádnému závěru.
Poznámka: Právě jsme viděli to nejlepší a nejhorší na srovnávacím kritériu. Pokud funguje, tak je obvykle velice snadné se dobrat k výsledku. Je ale velice citlivé na malé změny a snadno selže.
Po pravdě řečeno, ten poslední příklad je tak snadný, že se při troše snahy dá udělat srovnávacím kritériem. Jsou dvě možné strategie. Pokud si myslíme, že daná řada diverguje, pak můžeme zkusit nějak zvětšit naši testovací řadu tak, aby divergovala, ale pořád ještě zůstala pod danou řadou, aby ji tak vytlačila nahoru. Pokud si na druhou stranu myslíme, že daná řada konverguje, pak namísto dolního odhadu potřebujeme získat horní konvergentní odhad, kterým bychom ji stlačili dolů.
Zkušenost naznačuje, že výraz
2k2 − 13 > k2.
Můžeme tedy odhadovat takto:
![]()
Protože řada napravo konverguje, daná řada také konverguje podle srovnávacího kritéria.
Právě jsme viděli, že s trochou představivosti se i to méně spolehlivé srovnávací kritérium dá k něčemu dostrkat. Často je ale jednodušší prostě použít jiné srovnání, které právě přichází.
Přímé srovnání používá nerovnost. Někdy můžeme také použít jiný způsob srovnání, když říkáme, že pro velká k jsou dvě věci v zásadě stejné. To má výhodu v tom, že taková situace je přirozeně symetrická, takže tvrzení půjdou v obou směrech. Nevýhoda je, že "jsou v zásadě stejné" je docela zrádné tvrzení, které je třeba upřesnit a v konkrétních případech doložit, což znamená více práce.
Věta (limitní srovnávací kritérium).
Uvažujme řady∑ ak a∑ bk splňujícíak > 0 a bk > 0 pro všechna k.
Předpokládejme, že
konverguje a
A > 0.
Pak∑ ak konverguje tehdy a jen tehdy, když∑ bk konverguje.
Jinými slovy,
Proč tam máme ten limitní předpoklad? V typickém případě, pokud je testovací
řada vybrána opatrně, dostaneme
![]()
Pokud je teď řada napravo konvergentní, pak je jejím součtem číslo, to se
vynásobí číslem A a dá to další číslo (zde využíváme toho, že
A není nekonečno), tudíž i řada nalevo by se měla nasčítat do čísla.
Pokud je řada napravo divergentní, pak je jejím součtem nekonečno a A
krát nekonečno je nekonečno (za předpokladu, že
Podobně odvodíme, že informace přechází zleva doprava, zase se jako špatné ukážou případy, kdy je A nulové nebo nekonečno, takže chápeme, proč je předpoklad věty vylučuje.
Příklad: Vyšetřete konvergenci
![]() .
.
Víme, že když je
k velké, tak členy této řady vypadají jako
Použijeme tedy limitní srovnávací kritérium. Tvrdíme, že když je k
velké, tak jsou dané členy v zásadě jako
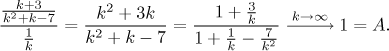
Potvrdili jsme, že náš odhad byl správný, takže se daná řada chová jako testovací řada, tedy jako harmonická řada. Protože tato řada diverguje, podle limitního srovnávacího kritéria i daná řada diverguje.
Symbolicky,
![]()
Poznámka: I zde by zkušený řadový detektiv našel způsob, jak použít srovnání, například tvrzením, že pro velká k platí
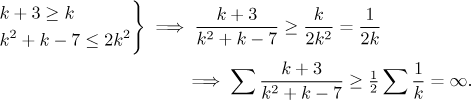
Tato nerovnost by se ovšem nejsnáze dokazovala právě přes limitu, takže se rovnou může jít na limitní srovnání.
Srovnávací kritérium a limitní srovnávací kritérium mají obecně jiné požadavky na testovací řadu. Když je nám dána řada a chceme na ni použít srovnání, tak se díváme po členech bk, které jsou vždy větší (nebo vždy menší) než dané ak. Tyto dva členy tedy nemusí být nutně podobné, rozdíl mezi nimi může být docela velký. Na druhou stranu, pokud chceme použít limitní srovnání, pak potřebujeme, aby testovací řada měla bk v zásadě stejné jako dané ak, ale nezajímá nás jejich vzájemná pozice. To naznačuje, že by nebylo úplně správné tvrdit, že jeden test je silnější než druhý, a opravdu se najde spousta řad, pro které jeden z nich funguje a druhý ne. Nicméně i v praxi funguje obyčejné srovnání lépe, když jsou bk podobné ak, jinak se začne testovací řada příliš lišit a dostáváme se do situace, kdy není možné udělat závěr. Pokud bychom například chtěli srovnáním dokázat, že nějaká řada konverguje, tak potřebujeme horní odhad, a pokud bychom šli nahoru příliš, tak ta testovací řada bude divergentní (nasčítá se do nekonečna) a skončili jsme. Vyplácí se tedy volit testovací řadu co nejbližší té dané.
Jsou i další testy, které používají srovnání, ale ve standardních kursech kalkulu se neprobírají. Jako příklad si ukážeme následující.
Věta.
Uvažujme řady∑ ak a∑ bk splňujícíak > 0 abk > 0 pro všechna k. Předpokládejme, že existuje celé číslo N takové, že pro všechnak > N máme
• Jestliže
∑ bk konverguje, pak také∑ ak konverguje.
• Jestliže∑ ak diverguje, pak také∑ bk diverguje.
Pro další informace viz Přehled metod - Srovnávací kritéria a Řešené příklady - Testování konvergence, jmenovitě tento příklad, tento příklad, tento příklad, tento příklad, tento příklad a tento příklad.