Definice.
Pod pojmem řada funkcí rozumíme symbol
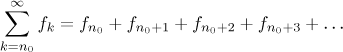
kde
Je-li dána řada funkcí, definujeme její obor konvergence jako
Definujeme její obor absolutní konvergence jako
Začneme s definicí řady funkcí a podíváme se na její konvergenci a stejnoměrnou konvergenci. Pak se podíváme na problematiku zachování vlastností.
Myšlenka funkčních řad se objeví přirozeně, když pracujeme s Taylorovými polynomy. Pro rozumné funkce zvyšování stupně Tn zlepšuje kvalitu aproximace, takže se zdá, že kdybychom nějak dokázali vytvořit nekonečný Taylorův polynom, dostali bychom přesně původní funkci. Nekonečný Taylorův polynom je nekonečná suma mocnin - tedy řada. V této a následujících sekcích ukážeme, že myšlenka nekonečných Taylorových polynomů opravdu funguje - ale je potřeba trochu práce k tomu, aby fungovala dobře.
Při vymýšlení pojmu řady pro funkce si přirozeně bereme inspiraci z řad čísel.
Definice.
Pod pojmem řada funkcí rozumíme symbol
kde
{ fk}k ≥ n0 je nějaká posloupnost funkcí.Je-li dána řada funkcí, definujeme její obor konvergence jako
{x reálné; ∑ fk(x) konverguje}. Definujeme její obor absolutní konvergence jako
{x reálné; ∑ fk(x) konverguje absolutně}.
Všiměte si, že definice má smysl. Pokud vezmeme nějaké reálné x,
které je v definičních oborech všech fk, a dosadíme
jej do všech těchto funkcí, pak
Protože pro každé x z oboru konvergence dostaneme číslo - součet
řady
Definice.
Uvažujme řadu funkcí∑ fk. Předpokládejme, že f je funkce definovaná na nějaké množině M a že všechny fk jsou také definovány na tomto M.Řekneme, že tato řada konverguje (bodově) k f na M, jestliže posloupnost částečných součtů
konverguje k f na M. Píšeme
Řekneme, že tato řada konverguje k f stejnoměrně na M, jestliže posloupnost
{sN} částečných součtů konverguje k f stejnoměrně na M. Píšeme
Obvykle samozřejmě chceme stejnoměrnou konvergenci a konvergenci na největší možné množině. Protože je konvergence řad založena na konvergenci posloupností (částečných součtů) a pro ně stejnoměrná konvergence implikuje bodovou konvergenci, tak okamžitě dostáváme následující.
Tvrzení.
Jestliže∑ fk ⇉ f na nějaké množině M, pak tam také∑ fk = f.
Správně bychom vlastně měli v tomto Tvrzení psát u sum limity, protože ta konkrétní funkce f rozhodně záleží na tom, kde indexace začíná. Kvůli stručnosti to obvykle vynecháme.
Než ukážeme příklad, zformulujeme řadovou verzi kritéria, které se ukázalo jako užitečné pro posloupnosti.
Tvrzení.
Uvažujme řadu funkcí∑ fk. Tato řada konverguje k nějaké funkci f stejnoměrně na množině M tehdy a jen tehdy, když
Příklad: Vyšetřete řadu
![]() .
.
Její členy xk jsou definovány pro všechna reálná
čísla, takže tam začneme. Nechť je x nějaké zvolené reálné číslo.
Pokud nejste zvyklí si takto hrát s x, klidně tomu číslu říkejte
c. Pak uvažujeme řadu
Dále si všimněte, že když je x z
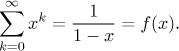
Teď bychom rádi zjistili, zda a kde je tato konvergence stejnoměrná. Připomeňme, že pro řadu se součtem f "stejnoměrná konvergence na množině M" znamená následující: Je-li dána tolerance, pak bychom měli být schopni najít částečný součet této řady, který aproximuje f na M v rámci oné tolerance. Abychom dostali inspiraci, podíváme se nejprve na obrázek f a několika částečných součtů dané řady.
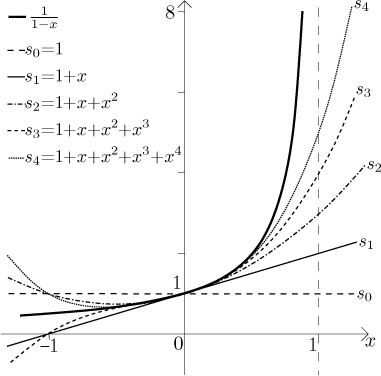
Zdá se, že máme potíže okolo 1. Dokonce i bez výpočtů můžeme říct, že
rozhodně nemáme stejnoměrnou konvergenci na celé množině
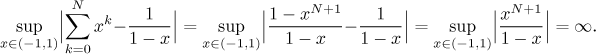
To, že je supremum nekonečné, se nejsnáze uvidí tak, že se vezme limita výrazu uvnitř v 1 zleva. Protože jsou všechna tato suprema nekonečná, nemohou konvergovat k 0, když pošleme N do nekonečna.
Vidíme, že problém je okolo 1, a také u −1 to nevypadá dobře (už jsme
diskutovali v předchozí sekci, že stejnoměrná konvergence bývá s otazníkem
na koncích množiny konvergence), takže co se stane, když ty konce odřízneme?
Uvažujme nějaké malé kladné číslo d, nechť
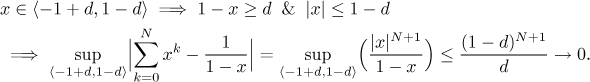
Zase jsme použili znalosti geometrické řady a fakt, že
Tento příklad je velmi poučný. Abychom mohli studovat stejnoměrnou
konvergenci, potřebujeme znát f, ale náš globální přístup nám to
nijak nepomůže najít. Je tedy nejprve třeba použít bodový přístup: Zvolí se
x a vyšetřuje se absolutní konvergence výsledné reálné řady, obvykle
pomocí odmocninového kritéria nebo podílového kritéria. Pokud máme štěstí,
tak zjistíme, že tato reálná řada konverguje k nějakému číslu
Teoreticky je situace pro posloupnosti a řady podobná, ale ve skutečnosti zde máme vážný problém. Víme, že rozeznat konvergenci řady je často relativně snadné, takže můžeme čekat, že běžně najdeme obor konvergence. Na druhou stranu, najít součet řady je většinou velice obtížné, takže nalezení f už čekat nemůžeme. Jak pak rozeznáme stejnoměrnou konvergenci? Nejpopulárnější odpověď je následující tvrzení.
Věta (Weierstrassova věta).
Uvažujme řadu funkcí∑ fk a množinu M. Předpokládejme, že existují reálná čísla ak taková, že∑ ak konverguje a
| fk(x)| ≤ ak pro všechna k a všechna x z M.Pak řada
∑ fk konverguje stejnoměrně na M.
Pomocí této věty snadno dokážeme stejnoměrnou konvergenci v zatím posledním
příkladě výše. Pro x a
Příklad: Vyšetřete řadu
![]() .
.
Když zvolíme nějaké x, pak se stane konstantou a můžeme výslednou řadu reálných čísel porovnat s nějakou známou p-řadou, abychom dokázali, že konverguje.
![]()
Nemáme ovšem žádnou představu, jaký je součet takové řady pro zvolené x. Víme tedy, že obor konvergence dané řady funkcí je celá reálná osa, ale neznáme její součet f a tudíž je nemožné zkoumat stejnoměrnou konvergenci přes suprema.
Weierstrassova věta ovšem funguje v pohodě, stačí vzít jako M množinu
všech reálných čísel a onen odhad výše naznačuje, že
Stále nevíme, k jaké funkci konverguje, což může vypadat srandovně, ale už jen vědět, že se někde děje stejnoměrná konvergence, nám umožňuje s řadou provádět spoustu užitečných věcí, jak uvidíme níže.
Věta (Dirichletovo kritérium stejnoměrné konvergence).
Uvažujme řadu funkcí∑ fk, jejíž částečné součty jsou stejnoměrně omezeny na množině M. To znamená, že existuje reálné číslo h takové, že pro všechna x z M a pro všechna N máme
Nechť
{gk} je posloupnost funkcí, která konverguje stejnoměrně k 0 na M. Pak řada∑ fkgk konverguje stejnoměrně na M.
Příklad: Vyšetřete řadu
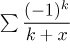 .
.
Když zvolíme nějaké
Teď bychom rádi ukázali stejnoměrnou konvergenci na M, ale
Weierstrassova věta tu nepomůže. Máme přirozený horní odhad
Připomeňme, že alternující
řada s členy
Věta (Abelovo kritérium stejnoměrné konvergence).
Uvažujme klesající posloupnost funkcí{ fk(x)}, která je stejnoměrně omezená na nějakém omezeném uzavřeném intervalu M; tedy existuje h takové, že| fk(x)| ≤ h pro všechna k a všechna x z M.
Nechť∑ ak je konvergentní řada reálných čísel. Pak řada∑ ak fk konverguje stejnoměrně na M.
Tuto část uzavřeme důsledkem Diniho věty z předchozí sekce. Všimněte si, že jestliže jsou všechny funkce dané řady nezáporné, tak její částečné součty tvoří neklesající (a tedy monotonní) posloupnost funkcí.
Věta (Diniho věta).
Uvažujme řadu funkcí∑ fk, která konverguje k nějaké funkci f na nějakém omezeném uzavřeném intervalu M. Jestliže jsou všechny funkce fk nezáporné na M, pak je tam konvergence řady stejnoměrná.
Konvergenci řad jsme definovali pomocí konvergence posloupností, takže se všechno, co jsme o vlastnostech napsali v předchozí sekci, přenáší i sem. Jak se dá čekat, řady se chovají dobře, když aplikujeme obvyklé algebraické operace.
Věta.
Předpokládejme, že řada funkcí∑ fk konverguje k funkci f na množině M a že řada funkcí∑ gk konverguje k g na stejné množině M. Pak platí následující tvrzení:
(i) Pro libovolné reálné číslo a řada∑ (a⋅ fk) konverguje ka⋅ f na M.
(ii) Řada∑ ( fk + gk) konverguje kf + g na M.
(iii) Řada∑ ( fk − gk) konverguje kf − g na M.
(iv) Řada∑ ( fk⋅gk) konverguje na M.
Stejně jako u reálných řad není bodový součin v (iv) příliš užitečný a dáváme přednost násobení funkčních řad jiným způsobem (Cauchyho součin). Vrátíme se k tomu v sekci o mocninných řadách.
Vlastnosti, které se zachovávaly u posloupností, se přirozeně také zachovávají zde.
Věta.
Předpokládejme, že řada funkcí∑ fk konverguje k funkci f na množině M.
(i) Jestliže jsou všechny fk liché, pak je také f lichá.
(ii) Jestliže jsou všechny fk sudé, pak je také f sudá.
(iii) Jestliže jsou všechny fk T-periodické, pak je také f T-periodická.
(iv) Jestliže jsou všechny fk neklesající funkce, pak je také f neklesající funkce.
(v) Jestliže jsou všechny fk nerostoucí funkce, pak je také f nerostoucí funkce.
(vi) Jestliže jsou všechny fk konstantní funkce, pak je také f konstantní funkce.
Z předchozí sekce víme, že nelze očekávat zachování spojitosti a dalších "lepších" vlastností z pouhé konvergence (a je snadné na to udělat příklady podobné těm z předchozí sekce), na to potřebujeme stejnoměrnou konvergenci.
Věta.
Uvažujme řadu funkcí∑ fk konvergující k funkci f.
(i) Jestliže jsou všechny fk spojité na množině M a∑ fk konverguje stejnoměrně k f na M, pak je také f spojitá na M.
(ii) Jestliže jsou všechny fk spojité na množině M a∑ fk konverguje stejnoměrně k f na M, pak pro každý interval⟨a,b⟩, který je podmnožinou M, platí
(iii) Předpokládejme, že všechny fk jsou spojité na intervalu M a že
∑ fk konverguje stejnoměrně k f na M. Zvolme nějaké a z M a pro x z M definujme
Pak
∑ Fk konverguje stejnoměrně k F na M.(iv) Jestliže jsou všechny fk spojitě diferencovatelné na množině M a řada jejich derivací
∑ fk′ konverguje stejnoměrně k nějaké funkci g na M, pak f je diferencovatelná na M af ′ = g.
Navíc∑ fk konverguje k f stejnoměrně na M.
Zase vidíme, že derivace trochu zlobí, dokonce ani stejnoměrná konvergence řady fk nestačí, abychom dostali něco rozumného, a musíme klást požadavky na derivace. Jak jsme diskutovali v předchozí sekci, tyto vlastnosti jsou vlastně tvrzeními o změně pořadí operací. Ukážeme to v následujícím tvrzení, které také ukazuje, že i bez znalosti součtu řady může být užitečné vědět o stejnoměrné konvergenci, což ospravedlňuje ony kritéria výše. Protože vlastně jen přepisujeme předchozí větu, rozhodli jsme se obětovat přesnost v zájmu jasnosti vyjádření.
Tvrzení.
Předpokládejme, že řada funkcí∑ fk konverguje stejnoměrně na intervalu M a také že∑ fk′ konverguje stejnoměrně na M, pokud je to třeba. Nechť a a b náleží do M. Pak