Příklad: Vyšetřete konvergenci následující mocninné řady:
![]()
Řešení:
Vidíme, že střed této mocninné řady je
1. Vyšetříme absolutní konvergenci řady
![]()
Zde není obvyklá volba - odmocninové kritérium - příliš moudrá kvůli tomu faktoriálu, dáváme přednost podílovému kritériu.
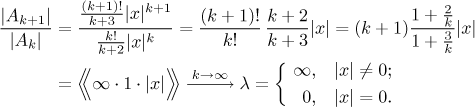
Víme, že řada konverguje absolutně, jestliže je lambda menší než 1, což se
zde stane, přesně když
2. Vyšetříme absolutní konvergenci řady
![]()
Zde budou fungovat dobře obě naše oblíbená kritéria, takže ať máme nějakou změnu, zkusíme odmocninové kritérium.
![]()
Víme, že řada konverguje absolutně, jestliže je ró menší než 1, což se zde
děje, přesně když
Protože víme, že poloměr konvergence součtu dvou řad je dán jako minimum
jednotlivých poloměrů (pokud si tedy nejsou rovny, což je naštěstí náš
případ), vychází nám z toho, že poloměr konvergence dané řady je
Interval konvergence je tedy
Závěr: Daná řada má střed
Poznámka o poloměru: Proč se u řad různými poloměry konvergence bere při
sčítání ten menší? Předpokládejme, že poloměry konvergence jsou
Pak se posuneme dále, a když jsme v mezikruží mezi poloměry R1 a R2, tak jedna řada konverguje a druhá diverguje, jejich součet je tedy na této oblasti divergentní. Podle věty o chování poloměru konvergence tedy poloměr konvergence součtu nemůže být větší než R1.
Pokud se posuneme ještě dál, za R2, tak by obě řady byly divergentní a obecně by se mohlo stát, že se v součtu důvody pro divergenci vykrátí a součet by tedy konvergoval. U mocninných řad to ale nepřipadá v úvahu. Víme, že pro ně konvergence v libovolném bodě už nutně znamená konvergenci na celém disku sahajícím až po tento bod, takže za oním mezikružím divergence už se vně nemůže nikde objevit konvergence.
Vidíme zároveň, že kdyby se poloměry rovnaly, tak už by toto mezikruží zaručené divergence neexistovalo, proto by už nic nebránilo tomu, aby se vně poloměru R1 = R1 dvě divergentní mocninné řady sečetly v konvergentní. To se opravdu stát může, pak je poloměr konvergence tohoto součtu větší než minimum poloměrů konvergence jednotlivých sčítanců.