Konvergence mocninných řad: Přehled metod

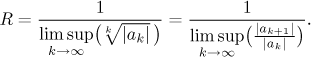
Je-li dána mocninná řada, tak víme, že konverguje na nějakém okolí svého středu (někdy i včetně některého z krajních bodů tohoto okolí). Její konvergenci lze tedy popsat pomocí těchto základních parametrů: Středu, poloměru konvergence, oboru absolutní konvergence a oboru konvergence. Někdy nás až tak moc nezajímá, co se děje v krajních bodech, pak první dvě data (střed a poloměr) stačí.

1. Určení středu. To je velice snadné. "Oficiální" tvar mocninné řady obsahuje členy (x − a)^k a toto a je střed. Jediná drobná komplikace může nastat, pokud je řada dána jiným způsobem, ale to se snadno napraví pomocí algebry (viz Příklad níže).

2. Určení poloměru konvergence. Toto se dělá vyšetřením absolutní konvergence dané řady.
Krok 1. Aplikujte absolutní hodnotu na členy řady a zjednodušte, mimo jiné by se v ní měl objevit člen |x − a|^k.
Krok 2. Použijte na tuto řadu buď odmocninové kritérium nebo podílové kritérium. V příslušná konstantě se ve většině případů (ale ne nutně) objeví |x − a|.
Krok 3. Ověřte konvergenci vyřešením nerovnice ϱ < 1, popřípadě λ < 1. Jestliže se v této nerovnosti objeví člen |x − a|, tak byste měli být schopni odvodit nerovnost typu |x − a| < R. Toto R je pak poloměr konvergence.
Pokud se člen |x − a| v podmínce konvergence neobjeví, pak je v typickém případě buď příslušná konstanta (ró nebo lambda) nula, což dává poloměr nekonečno, nebo je nekonečno (kromě středu), což dává poloměr nula.

Alternativa: Někteří lidé dávají přednost použití vzorce

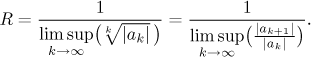
Nevýhodou je, že jej lze použít jen na řady v "oficiálním" tvaru, zatímco postup popsaný výše lze použít i na řady v jiném tvaru (viz příklad níže).

3. Určení chování v krajních bodech. Krajní body jsou a − R a a + R. Konvergence v nich se zjistí snadno, prostě se každý z nich dosadí do dané mocninné řady. Vždy z toho vyjde řada reálných čísel, která se pak vyšetřuje obvyklým způsobem, viz Přehled metod pro Testování konvergence. Všimněte si, že nemá smysl používat odmocninové kritérium či podílové kritérium, protože nutně vyjdou neurčité (poloměr z bodu 2 je přesně místo, kde tyto dva testy přestanou dávat informace).
Toto samozřejmě platí jen pro případ kladného R, pro R nulové či nekonečné žádné krajní body nejsou.

4. Obor konvergence. Pokud je poloměr konvergence kladný, pak obor konvergence je interval daný středem a poloměrem, (a − R,a + R), s přidanými krajními body, které vedly na konvergentní řadu v předchozím kroku.
Ten otevřený interval výše je obvykle také oborem absolutní konvergence. Jediná výjimka je v případě, kdy dostaneme konvergenci v obou krajních bodech, v kterémžto případě je obvykle oborem absolutní konvergence uzavřený interval a souhlasí s oborem konvergence.
Jestliže R = 0, pak je obor konvergence a obor absolutní konvergence stejný, je to jednobodová množina {a}.
Jestliže R = ∞, pak je obor konvergence a obor absolutní konvergence stejný, je to množina reálných čísel.

Poznámka: Často dostáváme mocninnou řadu, která není ve správném tvaru, což obvykle znamená, že namísto (x − a)^k obsahuje členy (Ax − B)^k. Taková řada se snadno přepíše do tvaru vzorové mocninné řady a pak se použije výše popsaný algoritmus(viz Příklad níže), ale obvykle je rychlejší ten algoritmus aplikovat přímo na řadu, jak je zadána.

Příklad: Vyšetřete konvergenci řady

Nejprve řadu přepíšeme, aby byla v příslušném tvaru.

Její střed je tedy a = −2. Teď na její členy aplikujeme absolutní hodnotu a zkusíme určit konvergenci pomocí odmocninového kritéria. Ve vzorci pro tento test použijeme A_k, protože v kontextu mocninných řad se a_k obvykle používá jen pro koeficienty, nikoliv pro celé členy řady.

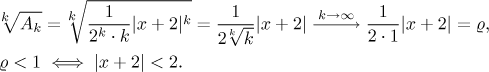
Dostáváme tedy poloměr konvergence R = 2.

Ze středu a poloměru konvergence vidíme, že krajní body jsou −4 a 0 (viz obrázek níže), teď se na ně podíváme.

x = −4: Dosadíme do dané řady (jak jsme si ji přepsali) a dostaneme

Toto je slavná alternující harmonická řada, o které víme, že konverguje podle Leibnizova kritéria, viz příklad zde.

x = 0: Dosadíme do dané řady a dostaneme

To je stejně slavná harmonická řada, o které víme, že diverguje (nebo použijeme p-test).

Závěr: Obor konvergence je interval ⟨−4,0), obor absolutní konvergence je interval (−4,0).

Pro někoho je to snažší, když si nakreslí obrázek, do kterého postupně doplňuje data.

Poznámka: Řada v našem příkladě nebyla zadána ve správném tvaru. Jak by se aplikoval výše popsaný algoritmus přímo na ni, jak je zadána?

Střed se najde vyřešením rovnice 2x + 4 = 0.

Konstanta ϱ se najde podobně jako předtím.

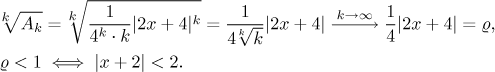
Takovýto postup je obvykle jednodušší. Pokud jste však zvyklí hledat poloměr konvergence pomocí vzorce, pak řadu nutně musíte nejprve upravit na předpisový tvar.

Pro další příklady viz Řešené příklady - Řady funkcí.

Rozvoj v mocninnou řadu
Zpět na Přehled metod - Řady funkcí