Příklad: Rozviňte danou funkci v mocninnou (Taylorovu) řadu s daným středem.

Řešení: Arkus sinus není funkce, jejíž řadu bychom si pamatovali. Potřebujeme tedy najít nějaké spojení mezi touto funkcí a kvartetem, který si pamatujeme. Evidentně se z těch čtyř funkcí nedá arkus sinus dostat pomocí algebraických operací. Jedna možnost je použít Lagrangeův inverzní vzorec aplikovaný na arkus sinus coby inverzní funkci k sinu. Je to ale tak hnusné (viz níže), že si to necháme jako poslední zoufalou možnost.

Můžeme také zkusit jiné způsoby, jak spolu svázat funkce, například diferenciální počet. Integrál z arcsin(x) je ještě horší, což takhle derivace?

Coby zlomek to připomíná vzorec pro součet geometrické řady, ale ta odmocnina navíc je nepřekonatelný problém. Druhý výraz, ten se zápornou mocninou, je již slibnější, protože zapadá do vzorce pro binomický rozvoj (ktrý si moc lidí nepamatuje; rozhodně je méně populární než ony základní čtyři funkce, ale zde už nemáme na výběr). Poslední výraz je na to připraven. Všimněte si, že rozvoj platí pro |y| = |-x²| < 1.

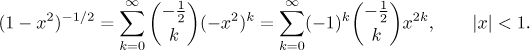
Abychom dostali arkus sinus, budeme integrovat. Jsou dvě možnosti. Jedna je integrovat pomocí určitého integrálu s proměnnou jako horní mezí (pak je dobré změnit proměnnou v našem rozvoji na t), což dává

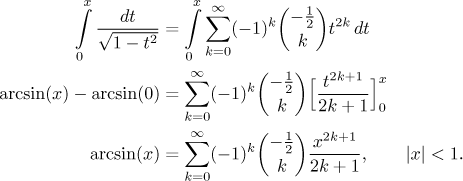
Druhá alternativa je použít neurčitý integrál:

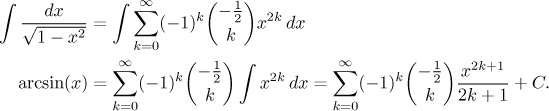
Potřebujeme určit C, ale to je snadné. Ona rovnost výše by měla platit pro všechna x splňující |x| < 1, takže si jedno takové x vybereme a dosadíme do obou stran. Zde se zdá x = 0 jako dobrý nápad, vyleze z toho rovnice 0 = C. Dostáváme tedy stejný rozvoj.

Ta řada vypadá docela pěkně, ale hodně lidí by se zeptalo na ta kombinační čísla a měli by pravdu. Stojí tedy za to zkusit najít přátelštější verzi.

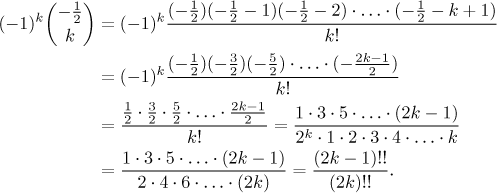
(Připomeňte si dvojitý faktoriál, viz Funkce - Teorie - Elementární funkce.) Tohle už vypadá docela dobře, takže můžeme odpověď napsat jako

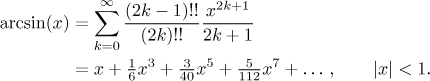
Poznámka: Jak bychom to řešili pomocí Lagrangeova inverzního vzorce? V našem případě dává

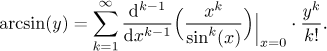
Derivace obecného řádu (k − 1) se nedá rozumně vypočítat, protože se neřídí nějakým rozumně zjistitelným vzorem, takže nejlepší, co se dá dělat, je spočítat prvních pár členů z počátku rozvoje. Všimněte si, že dosazování x = 0 do derivace se dělá v případě nutnosti skrz limitu (dělíme tam nulou, takže se hodně použije l'Hôpitalovo pravidlo).

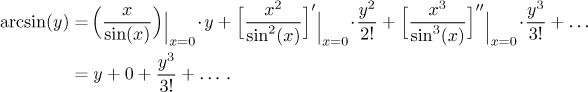
Zdá se, že se to shoduje s naším výsledkem, ale jít dál by byla ztráta času, už i ta druhá derivace byla dost hnusná.

Další příklad
Zpět na Řešené příklady - Řady funkcí