Příklad: Pro následující funkci najděte její Fourierovu řadu, sinovou Fourierovu řadu a kosinovou Fourierovu řadu; pro každou řadu určete její součet.
![]()
Řešení: Toto vypadá jako standardní příklad, takže použijeme obvyklý postup.
Fourierova řada:
Když danou funkci rozšíříme periodicky, bude její perioda
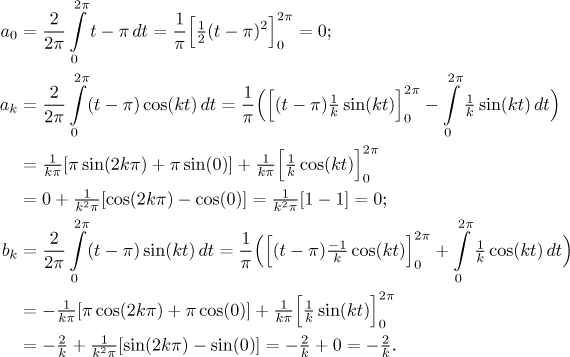
Dostaneme tedy
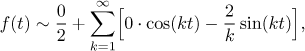
neboli
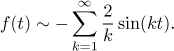
K nalezení součtu této řady použijeme Jordanovy podmínky. Nejprve nakreslíme periodické rozšíření dané funkce f a pak ve všech bodech nespojitosti umístíme tečky na úrovních, které tam průměrují levé a pravé limity.

Sinová Fourierova řada:
Vzhledem k tomu, že v získané Fourierově řadě vystupují pouze siny, tak už
to je sinová řada. Dalo se to čekat vzhledem k tomu, že periodické
rozšíření, které jsme si nakreslili, je lichá funkce, takže je to
automatické.
Co by se stalo, kdybychom aplikovali standardní postup pro získání sinové Fourierovy řady? Nakonec bychom dostali stejný výsledek.
Sinovou Fourierovu řadu dostaneme tak, že uvažujeme rozšíření dané funkce
f na interval
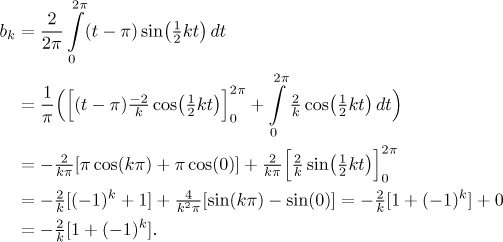
Dostaneme tedy
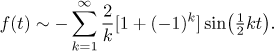
Všimněte si, že výraz
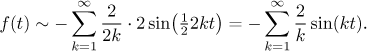
Dostali jsme stejnou řadu jako předtím. Abychom určili její součet, tak nejprve nakreslíme liché periodické prodloužení f, ale všimněte si, že v tom obrázku výše už prodloužení f liché je, takže ten obrázek platí i zde.
Kosinová Fourierova řada:
Teď použijeme standardní postup k nalezení kosinové Fourierovy řady.
Dostaneme ji rozšířením dané funkce f na
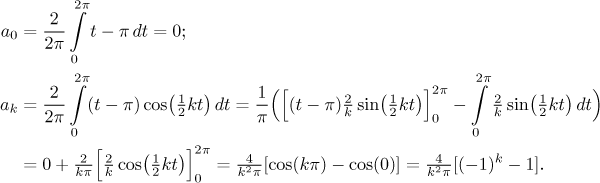
Dostaneme tedy
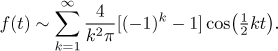
Všimněte si, že výraz
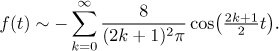
Abychom určili součet této řady, začneme nakreslením sudého rozšíření f, pak bychom měli zpracovat body nespojitosti, ale protože tam žádné nejsou, tak víme, že kosinová Fourierova řada konverguje k tomuto rozšíření a tato konvergence je stejnoměrná na reálné ose.
