Problem: Expand the given function in a power (Taylor) series with the given center:

Solution: The arcsine is not a function whose series we would remember. Thus we need to find come connection between this function and the quartet that we do remember. There is no way to get arcsine using some algebraic operations from the four functions. One possibility is to use the Lagrange inverse formula applied to arcsine as the inverse function to sine. However, here it is really bad (see below), so we will leave this as the last resort.

We can also try other means of linking functions, for instance differential calculus. Integral of arcsin(x) is even worse, what about the derivative?

In the form of fraction it resembles the formula for the sum of geometric series, but the extra square root is an insurmountable obstacle. The second expression, with negative power, is more promising, since it fits the pattern for the binomial expansion (which not too many people remember; it is definitely less popular than the basic four functions, but here we have no other choice). The last expression is ready for it. Note that this expansion is valid for |y| = |-x²| < 1.

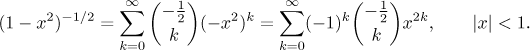
To get to arcsine we need to integrate. There are two possibilities. One is to integrate using a definite integral with variable as the upper limit (then it is good to change the variable in our expansion to t), which yields

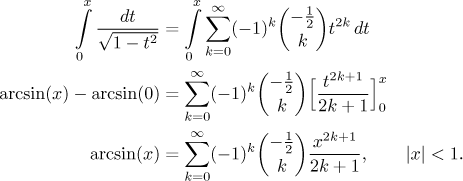
The other alternative is to use indefinite integral.

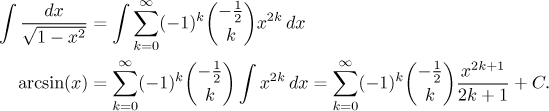
We need to determine C, but that is quite simple. The above equality is supposed to be true for all x with |x| < 1, so we choose one such x and substitute to both sides. Here x = 0 seems like a good idea, yielding the equation 0 = C. Thus we obtain the same expansion.

The series looks quite nice, but many people would ask about those combinatorial numbers and they would be right. Thus is it worthwhile to try and find a more friendly version.

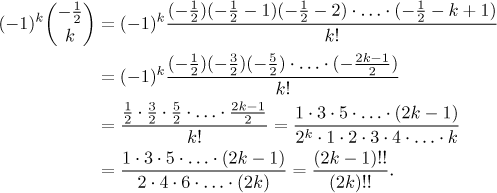
(Recall the double factorial, see Functions - Theory - Elementary functions.) This looks quite nice, so the answer can be stated as

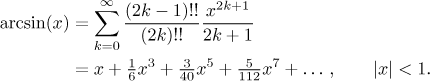
Remark: How would it go using the Lagrange inversion formula? In our case it goes

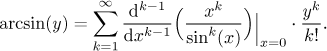
The derivative of general order (k − 1) cannot be figured out easily as it does not follow any readily recognizable patter, so the best we can do is to try at least some terms at the beginning of the series. Note that the substitution of x = 0 into the derivative is done by limit when necessary (we have division by zero there, so l'Hôpital's rule is used a lot).

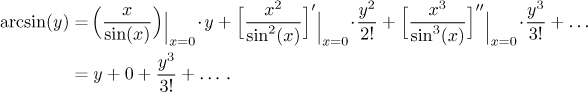
This seems to fit our result above but to go any further is a waste of time, already the second derivative was quite ugly.

Next problem
Back to Solved Problems - Series of functions