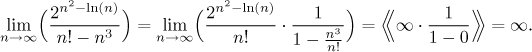Příklad: Najděte následující limitu (pokud existuje)

Řešení: Vidíme, že máme podíl mocnin, takže bychom rádi použili intuitivní výpočet; bohužel je ale v čitateli malý problém. Kdyby byl čitatel jen součet n² − ln(n), věděli bychom, co dělat; bohužel, tento výraz je dán do exponenciály, což znamená, že intuitivní úvahy už neplatí. Co můžeme dělat?

Ve jmenovateli víme, že když je n hodně velké, pak n³ je zanedbatelné vzhledem k faktoriálu n! a můžeme to ignorovat. Víme také, že ln(n) je zanedbatelný vzhledem k n², ale protože tohle se děje v exponentu, je to poněkud zrádné. Víme, že ignorováním ln(n) bychom udělali jen malou chybu pro velká n, pak ale uděláme "2 na mocninu rovnou této malé chybě" a nemáme ponětí, co se stane.

Když nevíme, co dělat, je obvykle lepší začít jednodušším příkladem a pak zjistit, jestli to, co se dozvíme, také nepomůže u toho komplikovanějšího. Začneme tedy zkoumáním

Škála mocnin říká, že "faktoriály přebijí exponenciály", to ale platí pouze pro věci jako 2ⁿ. Víme, že násobky v exponentu nevadí, například lze použít 2³ⁿ = (2³)ⁿ = 8ⁿ a faktoriál by to pořád porazil, jenže druhá mocnina je něco úplně jiného. Není způsob, jak změnit algebraicky 2ⁿ² na něco typu aⁿ.

Jsme tedy nuceni s lítostí dojít k závěru, že škála mocnin nám nedá odpověď. Přesto ale pomůže. Když jsme ji dokazovali, důkazy používaly párování a srovnání. Zde máme dvě věci. Faktoriál n!, což je součin n věcí (čísla 1, 2,..., n), a 2ⁿ², což je součin věcí (dvojek). Mohli bychom tato dvě čísla nějak chytře spárovat? Můžeme zkusit tohle:

Jak velké je toto číslo? Všimněte si, že všechny ty zlomečky jsou nejméně jedna, protože 2ⁿ > n. Pokud toto použijeme pro všechny členy kromě posledního, dostaneme

Poslední fakt vyplývá ze škály mocnin a dá se dokázat pomocí l'Hospitalova pravidla. Práve jsme pomocí srovnání dokázali, že zjednodušená posloupnost jde do nekonečna:

Teď tam vecpeme tu část n³ a tvrdíme, že ji faktoriály přebijí, a tak je zanedbatelně malá, pořád ještě máme

Jak bychom toto dokázali? Jsou dvě možnosti, Tradiční přístup z šuplíku polynomy a podíly s mocninami je vytknutím dominantních členů. Dostaneme

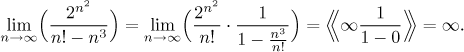
Nula při vyhodnocování jmenovatele vyplývá ze škály mocnin, "faktoriály přebijí mocniny." Jak bychom to dokázali, kdyby to bylo třeba? Dělá se to srovnáním (faktoriál se nedá derivovat, takže l'Hospital je rozhodně mimo hru, a jiná možnost se zrovna nenabízí).

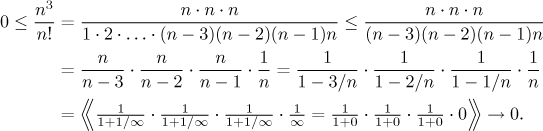
To uzavřelo důkaz, že opravdu

Další způsob, jak dovnitř vpašovat n³, je využít přístup z poznámky o intuitivním výpočtu. Funguje to následovně: dvě posloupnosti mají tutéž limitu, jestliže jejich podíl konverguje k 1. Stačí tedy porovnat ty dvě posloupnosti, s a bez n³.

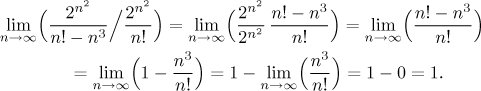
Všimněte si, že to bylo velmi podobné předchozímu výpočtu a použil se stejný pomocný fakt o podílu n³/n!.

Popravdě řečeno, existuje mnohem snadnější způsob. Protože chceme ukázat, že tato posloupnost jde do nekonečna, stačí najít vhodný dolní odhad pomocí již známého výsledku. Ale to je snadné, z nerovnosti n! − n³ < n! dostaneme

2ⁿ²/(n! − n³) > 2ⁿ²/n!→∞.

Všimněte si, že kdyby ve jmenovateli bylo "+", toto srovnání by už nefungovalo:

2ⁿ²/(n! + n³) < 2ⁿ²/n!→∞.

Toto říká, že posloupnost nalevo má limitu nejvýše rovnou nekonečnu (pokud existuje), ale to nechává příliš volnosti - všechno je menší či rovno nekonečnu, posloupnost nalevo může klidně i oscilovat (a tak nemít limitu), nebo může jít do nekonečna, jen pomaleji než ta napravo, což se ve skutečnosti děje! Jak by se to dokázalo? Snadno, první dva důkazy, které jsme použili, také fungují s "+" ve jmenovateli.

To už stačí o tomto pomocném kroku. Teď bychom rádi nějak vpašovali dovnitř ln(n). Bohužel, naše předchozí podezření, že věci nejsou tak snadné, se ukáže správné, když to zkusíme. Jmenovitě, mohlo by být pravda, že 2ⁿ² a 2^{n2 − ln(n)} jsou okolo nekonečna zhruba stejné? Podíváme se na jejich podíl a zjistíme, že to není pravda:

Toto ukazuje, že 2ⁿ² je neporovnatelně větší okolo nekonečna než 2^{n2 − ln(n)}. Jak tedy přejdeme od posledního dokázaného výsledku k limitě, kterou opravdu hledáme? To, co jsme zatím udělali, nejde použít jako pomoc:

Dostali jsme neurčitý podíl a nemůžeme aplikovat l'Hospitalovo pravidlo, protože neumíme derivovat faktoriál. Algebraicky tedy neumíme přejít od známého k danému.

Což takhle srovnání? Máme n² − ln(n) < n², takže můžeme zkusit následující:

Bohužel, z tohoto typu srovnání nemůžeme udělat žádný závěr. Pokud má hledaná posloupnost limitu, měla by být menší nebo rovno nekonečnu (musíme přejít na "menší nebo rovno", srovnání nefunguje pro ostré nerovnosti), což znamená, že může být prakticky cokoliv, včetně možnosti, že nemá vůbec limitu.

Vidíme tedy, že nelze přejít od známého výsledku k dané posloupnsti přímo, musíme ji řešit nezávisle na posledním výsledku. Nicméně příklady jsou tak podobné, možná dostaneme nějakou inspiraci z toho, co už jsme udělali.

Jedna možnost je použít faktu, že n je nakonec mnohem větší než ln(n). Všimněte si, že v předposledním výpočtu jsme měli 2ⁿ² v čitateli a 2^ln(n) ve jmenovateli, a víme ze škály mocnin, že to první převáží nad druhým. Bohužel už jsme vyčerpali 2ⁿ² k "přebití" faktoriálu ve jmenovateli. Když se nicméně podíváte na příslušné srovnání nahoře, uvidíte, že ty nerovnosti tam byly dost kavalírské, docela dost jsme v tom odhadu ztratili. Možná tedy nepotřebujeme celé 2ⁿ² k přebití faktoriálu. Dalo by se "půjčit" kousek 2ⁿ² a přebít také tu část s logaritmem? Zkusíme to:

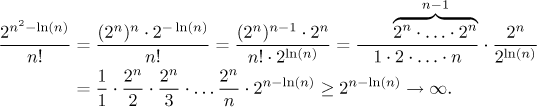
V poslední nerovnosti jsme použili toho, že 2ⁿ/2 > 1, 2ⁿ/3 > 1,..., 2ⁿ/n > 1. Závěr o limitě pak následuje z faktu, že n² − ln(n) konverguje do nekonečna (viz například sekci o intuitivním výpočtu) and 2^∞ = ∞. Srovnání teď jde správným směrem a vyplývá z něj, že

Přesně jako předtím, teď už není problém propašovat do jmenovatele n³ a dokázat například srovnáním, že

Další příklad
Zpět na Řešené příklady - Limita