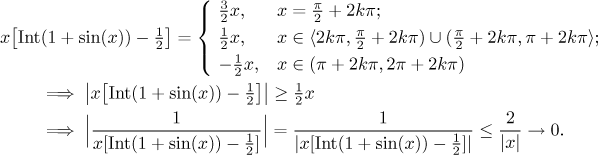Zde se podíváme blíže na několik zajímavých situací s oscilací. Předpokládá se, že se čtenář už podíval na předchozí příklad. Formální a úplné důkazy zde přeskočíme, raději si zde zkusíme trochu zlepšit intuitivní chápání. Formální důkazy by byly velice podobné těm z předchozího příkladu, buď se dokazuje limita srovnáním, nebo neexistence pomocí Heineho věty.

Příklad: Najděte (pokud existuje)

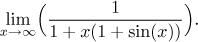
Řešení: Chování výrazu x(1 + sin(x)) jsme už zkoumali v předchozím příkladě, takže víme, osciluje mezi 0 a 2x, jak se blížíme k nekonečnu s x. Také je to vždy kladné nebo nula, takže 1 + x(1 + sin(x)) je přinejmenším 1 a osciluje mezi 1 a 1 + 2x. Proto když to dáme do jmenovatele zlomku s jedničkou nahoře, bude tento zlomek oscilovat mezi 1 a 1/(1 + 2x). Protože to druhé jde v nekonečnu k nule, pro opravdu velké hodnoty x daný výraz osciluje mezi 1 a "skoro 0", takže odhadneme, že limita neexistuje. Abychom to dokázali, stači uvažovat posloupnosti x_n = π/2 + 2nπ a y_n = 3π/2 + 2nπ. Situace vypadá v zásadě takto:

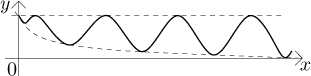
Poznámka: Do jmenovatele jsme museli přidat "1 +", protože výraz x(1 + sin(x)) je nulový v nekonečně mnoha bodech jdoucích do nekonečna. Neexistovalo by tedy žádné okolí nekonečna, kde by výsledný zlomek existoval, a nešlo by tam dělat limitu. To není problém u následujícího výrazu.

Příklad: Najděte (pokud existuje)

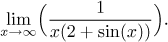
Řešení: Sinus osciluje mezi 1 a −1, takže 2 + sin(x) osciluje mezi 1 a 3 včetně. Proto x(2 + sin(x)) osciluje mezi x a 3x, mimo jiné to tedy jde do nekonečna. Následně 1 dělená tímto výrazem jde k nule. Jak by se to dokázalo? Když jde výraz s omezenou oscilací k nule, jako nejlepší se zdá verze Věty o sevření s absolutní hodnotou. V nekonečnu máme.

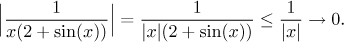
Mimochodem, když porozumíme, jak se chová 2 + sin(x), tak už snadno uhodneme, že

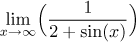
neexistuje (zlomek osciluje mezi 1 a 1/3) a že

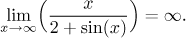
Zde bychom použili jednostranné srovnání, daný výraz můžeme odhadnout zdole pomocí x/3 a tak to vytlačit vzhůru.

Příklad: Najděte (pokud existuje)

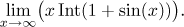
Řešení: Výraz 1 + sin(x) osciluje mezi 0 a 2 včetně, takže když na to aplikujeme funkci Int, dostaneme konstantní kousky s hodnotami 0, 1 a 2.

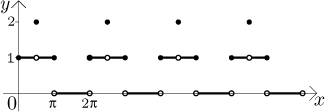
Když tohle vynásobíme x, dostaneme šikmé úsečky, které leží na přímkách y = 0, y = x a y = 2x.

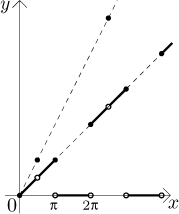
Proto limita neexistuje.

Mimochodem, co se dá říct o výrazu Int(0.9 + 0.9sin(x))? Výraz 0.9 + 0.9sin(x) osciluje mezi 0 a 1.8 včetně, takže když na to aplikujeme funkci celá část, dostaneme úsečky na úrovních 0 a 1. Jsou zde tedy dva rozdíly v porovnání s předchozím příkladem. První rozdíl je, že teď už máme jen dvě hodnoty, zbavili jsme se těch jednobodových teček na úrovni 2, které jsme předtím měli a které mohou zlobit. Jedno možné použití je ve výrazu

1/2 − Int(0.9 + 0.9sin(x)),

který teď má dvě různé hodnoty, −1/2 a 1/2.

Druhý rozdíl je v tom, že úsečky na úrovni 0 jsou teď delší než úsečky na úrovni 1, na rozdíl od předchozího případu, kde byl pěkně pravidelný obrázek.

Abychom to uzavřeli, výraz x⋅Int(0.9 + 0.9sin(x)) dává úsečky, které leží střídavě na přímkách y = x a y = 0.

Limita tohoto výrazu v nekonečnu proto neexistujue.

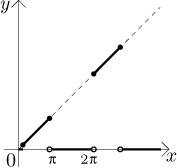
Příklad: Najděte (pokud existuje)

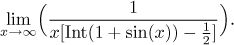
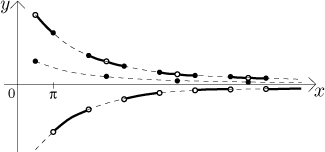
Řešení: Víme, že Int(1 + sin(x)) je funkce, která se sestává z úseček na úrovních 0, 1 a 2 (tam jsou jen tečky). Když odečteme 1/2, dostaneme funkci, jejíž graf jsou úsečky na úrovních −1/2, 1/2 a 3/2. Proto se graf funkce x[Int(1 + sin(x)) − 1/2] sestává z úseček, které leží na přímkách y = −x/2, y = x/2 a y = 3x/2.

Protože graf neustále skáče mezi přímkami, které jdou do nekonečna, a přímkou, která jde do mínus nekonečna, vyplývá z toho, že nemá limitu v nekonečnu. Co se stane, když tímto výrazem vydělíme jedničku? Daný výraz je občas roven −2/x, někdy 2/x a někdy 2/(3x). Všechny tři křivky jdou v nekonečnu k nule, takže každá funkce, která mezi nimi skáče, musí jít také k nule.

Jak by se to dokázalo? Protože máme oscilující výraz s omezenými částmi, tipneme si, že by pomohlo srovnání. Protože chceme dokázat, že něco jde k nule, jako nejlepší se zdá verze Věty o sevření s absolutní hodnotou.

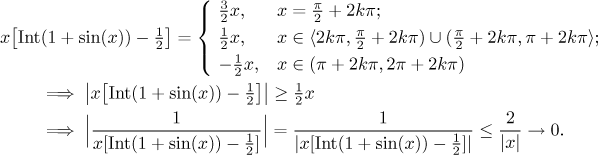
Další příklad
Zpět na Řešené příklady - Limita