Příklad: Najděte (pokud existuje) limitu

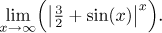
Řešení: Je to standardní problém, máme najít limitu v nekonečnu výrazu, který existuje na okolí nekonečna (všimněte si, že 3/2 + sin(x) > 0, takže nebudeme mít problém, když tuto obecnou mocninu změníme na její kanonický tvar "e na ln"). Začneme tedy dosazením nekonečna do výrazu.

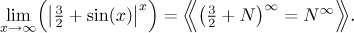
Výraz N^∞ je neurčitý (viz algebra N). Když tuto obecnou mocninu přepíšeme na kanonický tvar, dostaneme e^{xln(3/2 + sin(x))}, po dosazení nekonečna dostaneme v exponentu ∞⋅ln(N), což nám nikterak nepomohlo.

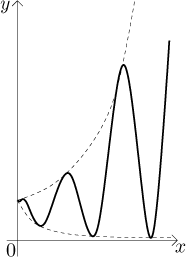
Standardní postupy tedy selhaly a je třeba se na výraz podívat blíže. Co se stane, když jde x do nekonečna? Výraz 3/2 + sin(x) neustále osciluje mezi 1/2 a 5/2 a my umocňujeme tento výraz na mocninu x. Výraz tedy občas vypadá jako (1/2)^x, jindy jako (5/2)^x, většinou vypadá jako něco mezi (ve skutečnosti graf daného výrazu osciluje mezi těmito dvěma exponenciálami).

Protože |1/2| < 1, exponenciála (1/2)^x jde v nekonečnu k nule. Na druhou stranu, protože 5/2 > 1, exponenciála (5/2)^x jde v nekonečnu do nekonečna. Daný výraz osciluje mezi těmito dvěma křivkami, odhadli bychom tedy, že nemá v nekonečnu limitu.

Jak by se to dokázalo? Nejjednodušší je použít Heineho větu. Budeme uvažovat dvě posloupnosti jdoucí do nekonečna. Pomocí jedné budeme skákat po vrcholech kopců, pomocí druhé po dolících, abychom ukázali, že daný výraz má dvě různé tendence pro x jdoucí do nekonečna.

Nejprve definujeme x_n = π/2 + 2nπ. Pak x_n→∞. Když toto dosadíme do daného výrazu f (x), dostaneme f (x_n) = (5/2)^{π/2 + 2nπ}→∞ pro n jdoucí do nekonečna.

Na druhou stranu definujme y_n = 3π/2 + 2nπ. Pak y_n→∞. Když toto dosadíme do daného výrazu f (x), dostaneme f ( y_n) = (1/2)^{3π/2 + 2nπ}→0 pro n jdoucí do nekonečna.

Kdyby měla f v nekonečnu limitu, pak by se ta limita musela rovnat zároveň nekonečnu i 0, což je spor.

Pro trochu jiný pohled na tento příklad se podívejte na tento příklad v části Posloupnosti - Řešené příklady - Limita.

Zpět na Řešené příklady - Limita