Základní vlastnosti, výpočet limity

Začneme tím, že se podíváme na několik základních vlastností limit. Pak se podíváme na věty používané při výpočtu limit. To vede přímo na algebru limit, náš hlavní nástroj k výpočtu limit. Další téma vede na jednostranné výsledky limit, což je také důležitá ingredience. Na konci sekce se podíváme na spojitost mezi limitou a některými vlastnostmi: omezenost, monotonie, posloupnosti atd.

Pár jednoduchých tvrzení

Následující tvrzení by vám měla být jasná, pokud chápete, co je to limita. Ve všech tvrzeních je a reálné číslo nebo (mínus) nekonečno.

Fakt.
Nechť je funkce f definována na nějakém prstencovém okolí bodu a. Pak f konverguje k L v a právě tehdy, když ( f − L) konverguje k 0 v a.

Fakt.
Nechť je funkce f definována na nějakém prstencovém okolí bodu a. Jestliže f jde k L v a, pak | f | jde k |L| v a.

Fakt.
Nechť je funkce f definována na nějakém prstencovém okolí bodu a. Pak f jde k 0 v a právě tehdy, když | f | jde k 0 v a.

Fakt.
Nechť jsou funkce f a g definovány na nějakém prstencovém okolí bodu a. a. Předpokládejme, že obě konvergují v a. Jejich limity v a jsou stejné právě tehdy, když f − g jde k 0 v a.

Poznamenejme, že poslední tvrzení neplatí, jestliže vypustíme předpoklad o konvergenci. Jako obvykle platí všechna tato tvrzení i pro jednostranné limity. Pro ty platí i tato věta:

Fakt.
Jestliže f má nenulovou limitu v a, pak existuje prstencové okolí U bodu a a konstanta k > 0 taková, že | f | > k na U.

Pro podrobnosti viz separace od 0 v sekci Spojitost v části Funkce - Teorie - Reálné funkce.

Když počítáme limity, vždy musíme začít něčím, co známe. Prvním takovým zdrojem limit je následující věta, jde vlastně jen o reformulaci věty, kterou už jsme měli předtím.

Věta (limita a spojitost).
Nechť f je funkce definovaná na okolí nějakého reálného čísla a. Jestliže je f spojitá v a, pak

Totéž platí pro jednostranné limity a jednostrannou spojitost, pak stačí mít existenci f na jednostranném okolí. Tato věta je velmi užitečná, protože víme, že všechny elementární funkce jsou spojité na svých definičních oborech, stejně tak jsou spojité funkce, které z těch elementárních dostaneme algebraickými operacemi.

Příklad: Limita  f (x) = x² − 3 v bodě a = 4 je f (4) = 13.

Příklad: Podíváme se na limitu v bodě 2 funkce

Tady nám věta jako taková nepomůže, protože g není dána nějakou jasně spojitou funkcí na nějakém okolí 2. Nicméně je dána výrazem x² na určitém levém okolí 2, proto můžeme najít limitu g v 2 zleva dosazením x = 2 do tohoto vzorce. Dostaneme

g(2^-) = 2² = 4.

Co víme o limitě zprava? Funkce g není dána nějakou jasně spojitou funkcí na pravém okolí 2, takže to nebude tak lehké. Je tomu ale tak pouze na první pohled. Všimněte si, že funkce h(x) = 2x je definovaná a spojitá na celé reálné ose, má tedy limitu v bodě 2 rovnou 2⋅2 = 4. Navíc tato funkce souhlasí s g na (2,∞), což je prstencové pravé okolí bodu 2. Proto je limita v bodě 2 zprava funkce g rovna limitě v 2 zprava funkce h, což je 4.

g(2⁺) = 4.

Protože limita g v bodě 2 zleva a zprava existují a rovnají se, následně existuje i limita funkce g v bodě 2 a je rovna 4.

Jak vidíme, větu lze použít i v obecnějších situacích, limitu funkce f v bodě a lze získat dosazením do nějakého výrazu, pokud je tento výraz spojitý v a a rovná se f na nějakém prstencovém okolí a. Analogická věc platí pro jednostranné limity.

Víme, že libovolný výraz, který vytvoříme z elementárních funkcí pomocí algebraických operací a skládání, je zase spojitý na svém definičním oboru a že to, zda a leží v onom definičním oboru, zjistíme prostě tak, že zkusíme dosadit a do tohoto výrazu. Odtud plyne následující pravidlo.

Základní pravidlo pro výpočet limity ve vlastních bodech.
Předpokládejme, že funkce f je definovaná určitým výrazem na nějakém prstencovém okolí reálného čísla a. Jestliže dosadíme a do tohoto výrazu a má to smysl, pak výsledek dává limitu f v a.

Příslušné modifikace platí také pro jednostranné limity. Pak stačí, aby bylo f definováno vhodným výrazem na nějakém příslušně jednostranném prstencovém okolí bodu a.

Připomeňme jeden triviální případ: Když dosadíme libovolné a do konstanty, dostaneme zase tu konstantu. V příkladě před chvílí jsme také viděli, jak se toto pravidlo používá dokonce i tam, kde funkce není dána jedním vzorcem, ale různými vzorci na každé straně a. V takovém případě přejdeme k jednostranným limitám a porovnáme výsledky. To se hodí obzvláště při práci s funkcemi danými rozpisem.

Toto pravidlo je velice užitečné; kdyby to tak ale fungovalo vždy, bylo by to moc lehké. Většinou se něco pokazí. Co se může pokazit? Jestliže f není definováno pěkným vzorcem na nějakém (jednostranném) prstencovém okolí bodu a, pak (s výjimkou opravdu podivných f ) tato funkce není vůbec definována na prstencovém okolí a a limitní otázka samotná nemá smysl. Proto jediným zajímavým případem zůstává situace, kdy f sice je definováno nějakým vzorcem na prstencovém okolí a, ale a samotné při dosazení do tohoto vzorce dělá problémy. Jinými slovy, a je přesně na hranici definičního oboru tohoto vzorce.

Tuto situaci lze rozšířit na případy, kdy je a nevlastní, my pak uvažujeme výraz, který je definován na okolí nekonečna a my chceme limitu v nekonečnu, podobně pro mínus nekonečno. Co pak můžeme dělat?

Některé případy jsou snadné. U všech elementárních funkcí víme, co se děje v koncových bodech intervalů jejich definičních oborů. Víme například, že limita ln(x) v a = 0 zprava je −∞. Krátce to můžeme zapsat jako ln(0⁺) = −∞. Podobně můžeme psát e^−∞ = 0 nebo tg((π/2)^-) = ∞. Pro souhrnný seznam viz algebra limit.

Je to zajímavější, když začneme dávat funkce dohromady. Potřebujeme vědět, jak skládat informace o limitách jednoduchých členů.

Věta (limita a algebraické operace).
Nechť a je reálné číslo, ∞ nebo −∞. Nechť f,g jsou funkce definované na nějakém prstencovém okolí a. Předpokládejme, že f má v a limitu A a g má v a limitu B. Pak platí následující:
(i) Pro libovolné reálné číslo c má funkce (c⋅f ) v a limitu c⋅A, jestliže to má smysl.
(ii) Funkce ( f + g) má v a limitu A + B, jestliže to má smysl.
(iii) Funkce ( f − g) má v a limitu A − B, jestliže to má smysl.
(iv) Funkce ( f⋅g) má v a limitu A⋅B, jestliže to má smysl.
(v) Funkce ( f /g) má v a limitu A/B, jestliže to má smysl.
(vi) Funkce f ^g má v a limitu A^B, jestliže to má smysl.

Co značí ta poznámka o smyslu? Jestliže jsou A a B reálná čísla, tj. pokud jsou ty dvě dané limity konvergentní, pak operace od (i) po (iv) mají smysl vždy. Podíl A/B má ale smysl jen pokud B není nula. Přesně tak je to myšleno. To, co jsme tu dostali, je vlastně rozšířením obvyklé algebry. Když jsme předtím napsali "3 + 2 = 5", měli jsme tím na mysli, že tři jabka přidaná k dvěma jabkům dají pět jablek. Teď to ovšem také může znamenat, že "když se posloupnost konvergující k 3 přičte k posloupnosti konvergující k 2, dostane se posloupnost konvergující k 5." Vzniká tak "algebra limit" a na rozdíl od algebry obvyklé, tato pracuje i s nekonečny.

Teď bychom mohli uvést větu se spoustami tvrzení, ale je mnohem lepší začít z opačného konce. Všimněte si, že v té větě výše jsme nikde nepředpokládali, že A,B jsou konečná, a některé operace lze definovat i pro případ, když se v nich vyskytuje nekonečno. Pokud ty operace použijeme v oné větě nahoře a považujeme je za "mající smysl", pak výsledky, které dostaneme, jsou správné. Jaké operace můžeme zavést?

Jestliže třeba f je (blízko a) ohromitánsky velká a g je zhruba 1, pak f − g pořád dává ohromné číslo (miliardář, který ztratí dolar, je pořád miliardář). Právě jsme "odvodili", že ∞ + L = ∞ pro reálná čísla L.
Co dostaneme, jestliže sečteme či vynásobíme dvě hrozně velká čísla? Další ohromně velké číslo. Právě jsme vymysleli, že ∞ + ∞ = ∞ a ∞⋅∞ = ∞.

Na druhou stranu nevíme, co je "∞ − ∞," protože odečtením dvou ohromných čísel můžeme dostat cokoliv. Takové výrazy se jmenují neurčité výrazy a dozvíte se o nich více v této poznámce. Odpovědi na tyto výrazy mohou být od "limita neexistuje" přes nevlastní limity až k vlastním limitám, je třeba je počítat individuálně.

To ukazuje, že "mít smysl" pro limity je trochu jiné než mít smysl pro čísla. Důvodem je, že čísla A,B teď nereprezentují reálná čísla, tj. pevné hodnoty, ale výsledky limit, jinými slovy, reprezentují procesy, "skoro čísla". To způsobuje, že některé operace, i když se dají dělat s reálnými čísly, nefungují s limitami. Nejlepším příkladem je mocnina 0⁰. Víme, že jako číslo to má smysl a dává to 1. Pokud ale tyto nuly reprezentují výsledky limit funkcí, pak jsme v situaci, kdy hledáme limitu obecné mocniny f ^g. Když se dostaneme blízko k a, pak jak f tak g jsou blízko nuly, ale malé číslo umocněné na malé číslo nemusí být blízko 1, může to být něco velice malého nebo naopak hodně velkého, podle toho která "skoro nula" je blíž nule.

Konec konců, v "normální" algebře platí, že pro (malá) kladná g je 0^g = 0, zatímco pro malá kladná f je f ⁰ = 1. Když pošleme f a g k nule, který z těchto dvou výsledků zvítězí? Výsledek limity (tj. výrazu 0⁰ v limitní algebře) nakonec závisí na tom, jak rychle jdou f a g k 0, limita dokonce ani nemusí existovat. 0⁰ je tedy neurčitý výraz.

Abychom to shrnuli, algebra limit nám umožňuje počítat komplikovanější limitu pomocí základních limit, stačí si jen pamatovat, co funguje, co určitě nefunguje a pak jsou tu neurčité výrazy, ty se musí dělat individuálně. Více detailů najdete v poznámce o algebře limit, nabízíme také stručný přehled.

Pořád jsme ještě neprobrali jednu důležitou operaci, jmenovitě skládání funkcí.

Věta (limita a skládání).
Nechť a je reálné číslo, ∞ nebo −∞. Nechť f je funkce definovaná na nějakém prstencovém okolí a, předpokládejme, že f má v a limitu A. Nechť g je funkce definovaná na nějakém prstencovém okolí bodu A, předpokládejme, že g má v A limitu B. Jestliže je splněna alespoň jedna podmínka z těchto dvou:
1. g je spojitá v A, nebo
2. existuje prstencové okolí a, na kterém f ≠ A,
pak je limita g( f ) v a rovna B.

Tato věta je trochu techničtější, pro praktické výpočty si stačí pamatovat, že jestliže f jde k A v a a g je spojitá (což platí pro většinu funkcí, které potkáme), pak dostaneme limitu g( f ) jednoduše jako g(A).

Příklad: Víme, že f = x² − 2x jde k 0 v a = 2. Víme také, že g = cos(x) je všude spojitá. Proto funkce g( f ) = cos(x² − 2x) jde k cos(0) = 1 v bodě a = 2.

To nám krásně ladí s přístupem "dosaď a uvidíš". Ony dvě věty o limitách a algebra limit nám umožňují rozšířit to základní pravidlo pro výpočet limit na všechny případy:

Jestliže chceme najít limitu v bodě a (který teď může být i nevlastní) určitého výrazu definovaného na prstencovém okolí a, pak "dosadíme" a do tohoto výrazu, a pokud má výsledek (získaný pomocí algebry limit) smysl (může být i nevlastní), pak je tento výsledek odpovědí na limitu.

To "dosadíme" jsme dali do uvozovek, protože nekonečno není opravdu číslo, takže to, co děláme, nemůžeme správně nazvat dosazením. Stejně tak není algebra limit "opravdovou" algebrou. Je sice možné ji udělat pořádně s definicemi a větami a vším, ale většina přednášejících to nedělá, takže je pak algebra limit jaksi ilegální, někteří profáci jsou dokonce alergičtí na to, když někdo zachází s nekonečnem jako s obyčejným číslem. Pro jistotu tedy dělejte výpočty s nekonečnem někde po straně; zde je ve výpočtech je spolu s dalšími poznámkami dáváme mezi velké dvojité lomené závorky ⟪ a ⟫, abychom naznačili, že nepatří do "oficiálního" řešení.

Poslední poznámka ohledně toho dosazování. Jestliže je ve výrazu obecná mocnina, měli bychom ji vždy přepsat do tvaru "e na ln".

Obě věty lze přepsat jiným způsobem. Můžeme je totiž použít k tomu, abychom odložili některé části limity na později, k rozdělení limity na části tak, abychom na každou mohli použít jinou metodu atd. Základní myšlenka je, že se věci dají "vytáhnout z limity", takže to, co v ní zbyde, bude jednodušší. První věta nám umožňuje vytahovat ven z limity algebraické operace za předpokladu, že to, co nakonec dostaneme, má smysl. Druhá věta nám umožňuje tahat z limity pěkné (spojité) vnější funkce, zase za předpokladu, že to, co dostaneme na konci, má smysl.

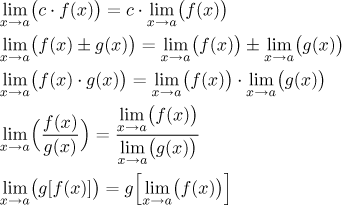
Příklad: Vypíšeme všechny detaily, aby bylo vidět, jak přemýšlíme. Zkušený student by napsal jen první a poslední řádek.

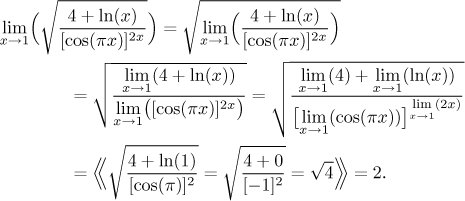
Tuto limitu bychom vlastně mohli spočítat metodou "dosaď a uvidíš", ale chtěli jsme ta pravidla ukázat na něčem jednodušším.

Poznamenejme, že ty rovnosti výše jsou "podmíněné". Když rozložíte limitu na několik částí, nevíte, jestli je tato rovnost pravdivá. Teprve až dokončíte výpočty všech menších částí, dáte jejich výsledky dohromady pomocí algebry limit a má to smysl, můžete říct, že ta rovnost byla dobře a výsledek je správnou odpovědí na původní limitu.

Pokud ale dokončíte jednotlivé limity a ukáže se, že jejich výsledky nejde spojit pomocí algebry limit, je ta podmíněná rovnost špatně a původní limita může být cokoliv. Jednoduchý příklad: Konstantní funkce 1 má v nekonečnu limitu 1. Když ji ale napíšeme jako 1 = (1 + x) − x a spočítáte limitu v nekonečnu každé části zvlášť, dostanete něco, co nemá smysl: ∞ − ∞.

Malá modifikace tohoto příkladu ukáže velice důležité pravidlo: Pokud si nejste naprosto jistí, že víte, co děláte, pak vždy dopočítejte všechny části. Například pokud rozdělíte limitu součinu na součin menších limit a jedna z nich vyjde nula, nemůžete přestat s výpočtem a prohlásit, že všechno je nula. Je sice pravda, že nula krát číslo je nula, ale to funguje jen v normální algebře. V algebře limit můžeme také mít "nula krát nekonečno", což je neurčitý součin, který může vyjít libovolně. Vrátíme-li se k předchozímu příkladu, můžeme to s limitou v nekonečnu zkusit i takto:

lim(1) = lim((1/x)⋅x) = lim(1/x)⋅lim(x) = 0⋅∞.

Evidentně by bylo chybou skončit, už když jsme viděli, že první limita vyšla nula, po dopočítání druhé části totiž vidíme, že máme neurčitý součin, a z toho víme, že nebyl dobrý nápad rozdělit původní limitu na dvě. Pro další detaily viz tato poznámka.

Při používání těchto pravidel a přístupů se dá narazit na několik problémů. Jeden z nich je, že použijete algebru limit a skončíte s neurčitým výrazem. Pak se musí použít rozličné triky na to, aby se zjistil výsledek. Některé triky najdete v následujících sekcích, praktický přehled užitečných metod lze nalézt v Přehledu metod.

Na další problém občas narazíme u jednostranných limit. Jmenovitě, když dosazujeme do některých funkcí, můžeme jít pouze z jedné strany, což by se nějak mělo odrazit v algebře limit. Například nemůžeme psát ln(0) = −∞, protože logaritmus neexistuje na nějakém prstencovém okolí 0. Existuje pouze na pravém prstencovém okolí 0, což jsme napsali jako ln(0⁺) = −∞. Co když máme do logaritmu dosadit nějaký výraz vedoucí na nulu?

Příklad: Podíváme se na limity f (x) = ln(x²) a g(x) = ln(x³) v a = 0. Pokud zkusíme použít algebru limit, v obou případech dostaneme ln(0). Nicméně první limita existuje a je rovna −∞, zatímco druhá dokonce ani nemá smysl. Funkce f má totiž za definiční obor všechna čísla kromě nuly, takže limita v 0 má smysl, a jak se blížíme k 0 s x, druhá mocnina změní x v ještě menší kladná čísla a výsledek je jasný. Na druhou stranu, funkce g je definována na (0,∞) a proto nemůžeme dělat limitu v 0.

Podobně se často dostaneme do problémů s výrazem 1/0. Z grafu 1/x víme, že limita v 0⁺ je ∞ a limita v 0^- je −∞. Tento fakt o jedné elementární funkci se také stane dalším pravidlem v algebře limit:

1/0⁺ = ∞     a     1/0^- = −∞.

V jednoduché přímočaré situaci s jednostrannou limitou prostě tato pravidla použijeme, ale co když máme ve jmenovateli funkci, která jde k nule? Například 1/x² a 1/x³ se okolo nuly chovají velice rozdílně. Také jiné funkce než ln(x) a 1/x vyžadují jednostranný přístup (tangens, kotangens atd.) Lze najít nějakou obecnou metodu, kterou bychom mohli použít pro řešení těchto příkladů nějak snadno?

Problém se spraví tím, že budeme uvažovat jednostranné výsledky limit. Probereme to v další části.

Jestliže chceme použít algebru limit i v situacích, kdy spolu skládáme funkce a vnější funkce vyžaduje jednostranný argument, dokážeme dostat odpověď jen v případě, kdy máme nějakou informaci o výsledku limity vnitřní funkce. To naznačuje, že bychom se měli blíže podívat na způsob, kterým je limitní hodnota dosahována. Porovnejme následující tři grafy:

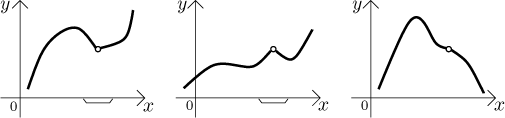
Ve všech třech případech je limita v a = 2 rovna 1, ale různými způsoby. V levém obrázku se k této limitě blížíme shora, tj. přibližujeme se k ní čísly většími než 1. Větší znamená napravo, takže řekneme, že se k limitnímu výsledku 1 blížíme zprava a označíme jej 1⁺ (dostáváme se k 1 od větších čísel, proto "plus"). V prostředním obrázku se k této limitní hodnotě přibližujeme zdola, tj. přibližujeme se k ní s čísly menšími než 1; takový výsledek značíme 1^- (jdeme k 1 od menších čísel, proto "mínus"). V posledním případě nemáme 1⁺ ani 1^-, je to prostě 1.

Definice.
Nechť a je reálné číslo, ∞ nebo −∞. Nechť f je funkce definovaná na nějakém prstencovém okolí bodu a, předpokládejme, že f má vlastní limitu L v a.
Označíme tuto limitu jako L⁺, jestliže existuje nějaké prstencové okolí a takové, že f > L na tomto okolí.
Označíme tuto limitu jako L^-, jestliže existuje nějaké prstencové okolí a takové, že f < L na tomto okolí.

Podobně definujeme L⁺ a L^- pro výsledky jednostranných limit.

Ve většině případů toto rozlišování nehraje roli, prostě řekneme, že limita je 1 a je to, ale někdy to může být velice důležité.

Vraťme se k příkladu výše, kde jsme se dívali na limitu v nule funkcí f (x) = ln(x²) a g(x) = ln(x³). Když se podíváme na vnitřní funkce x² a x³, vidíme, že v obou případech mají v 0 limitu 0, a když se toto pokusíme dosadit do logaritmu, nastane problém. Víme nicméně, že ln(0⁺) smysl má, což jasně naznačuje, že bychom se měli podívat blíže na výsledky limit x² a x³ v 0.

Když se x blíží k 0, pak funkce x² jde k 0 a také x² > 0. Výsledkem této limity je tedy 0⁺, proto můžeme dosadit do logaritmu:

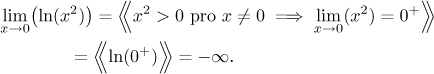
Na druhou stranu, i když je x velice blízko 0, pak x³ může být jak kladné, tak záporné, proto limita v 0 nemůže být zapsána jako 0⁺ nebo 0^-. Proto to nemůžeme dosadit do logaritmu, jasná indikace, že je něco v nepořádku s ln(x³) okolo 0.

Podobně teď snadno najdeme limitu 1/x² v 0, prostě dosadíme a použijeme algebru limit: Výsledek je

1/(0²) = 1/0⁺ = ∞.

Na druhou stranu, 1/x³ tak nelze spočítat. Co tedy dělat? Většinou se zkusíme podívat na jednostranné limity, protože pak informace navíc často dává jednostranné výsledky.

Příklad: Porovnejte následující dva příklady:

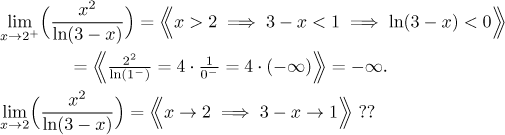
V prvním příkladě uvažujeme následovně: Když jde x k 2 zprava, znamená to, že x je něco jako 2 plus kousíček, řekněme 2.001. Pak (3 − x) je 1 mínus kousíček (pro x = 2.001 dostaneme 0.999). Když se aplikuje logaritmus na číslo menší než 1, stane se záporným. Tak odvodíme, že ta nula, kterou dostaneme obvyklým výpočtem ln(3 − 2), je ve skutečnosti "mínusová nula" a můžeme dosadit do zlomku.

Na druhou stranu, když jde x ke 2 z obou stran a dostane se blízko, pak je logaritmus skoro nula, ale někdy kladný a někdy záporný, podle toho, na jaké straně dvojky je x. Protože nejsme schopni blíže určit tu 0 ve jmenovateli, nemůžeme udělat žádný závěr. Dokonce právě to, že nejsme schopni donutit tu nulu, aby byla plusová nebo mínusová, nás vede k podezření, že limita nexistuje. Abychom to ověřili, zkusíme se podívat na limitu v 2 zleva:

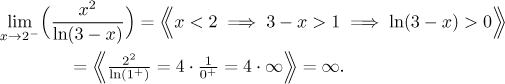
Protože limita v 2 zprava je jiná než limita v 2 zleva, dostaneme závěr, že limita v 2 neexistuje.

Poznámka: Ačkoliv se jednostranné výsledky často objevují u jednostranných limit, tyto dva pojmy nejsou ve skutečnosti nějak svázány. Je možné dostat jednostranný výsledek při výpočtu oboustranné limity, jednu takovou situaci jsme viděli, když jsme se dívali na limitu x² v 0. Na druhou stranu se také může stát, že máme jednostrannou limitu, ale výsledek jednostranný není. Například limita x⋅sin(1/x) pro x jdoucí k 0 zprava je 0, ale díky divoké a neustávající oscilaci se funkce nikdy neusadí na kladné či záporné straně, takže tento výsledek nemůže být 0⁺ nebo 0^-. Pro další informace o této funkci (například její graf) viz sin(1/x) v části Teorie - Elementární funkce.

Věta.
Jestliže funkce konverguje v nějakém bodě a, pak musí být omezená na nějakém prstencovém okolí a.

Tohle rozhodně neplatí naopak, příklad sin(1/x) v části Teorie - Elementární funkce ukazuje, že omezená funkce nemusí mít limitu, natož konvergovat. Tato věta má také příslušné verze pro jednostranné limity a jednostranná prstencová okolí.

Teď se podíváme na monotonii. Existence limity (nebo konvergence) neimplikují nic o monotonii, což se zdá jasné, víme totiž, že funkce může jít ke své limitě bláznivými způsoby. Z monotonie ale nějakou informací vyrazíme.

Fakt.
Funkce monotonní na nějakém levém prstencovém okolí bodu a má limitu v a zleva.
Funkce monotonní na nějakém pravém prstencovém okolí bodu a má limitu v a zprava.

Zde může být a také nevlastní. Dostaneme více, pokud spojíme monotonii a omezenost.

Fakt.
Funkce monotonní a omezená na nějakém levém prstencovém okolí bodu a má konvergentní limitu v a zleva.
Funkce monotonní a omezená na nějakém pravém prstencovém okolí bodu a má konvergentní limitu v a zprava.

Důsledek.
funkce, která je monotonní na intervalu, má nutně konvergentní jednostranné limity ve všech vnitřních bodech a také příslušné jednostranné limity v krajních bodech tohoto intervalu.

Zase to platí i pro nevlastní koncové body.

Začneme pěknou větou.

Věta (Heineho).
Nechť a je reálné číslo, ∞ nebo −∞. Předpokládejme, že funkce f má limitu L v a. Pak pro každou posloupnost {a_n} splňující a_n→a a a_n ≠ a platí f (a_n)→L.

Tuto větu jsme použili při práci s posloupnostmi. Věta také platí v opačném směru, ale pro hledání limit funkcí to není zrovna užitečné, protože bychom museli vyzkoušet všechny možné posloupnosti jdoucí k a, dosadit do f a podívat se, co se stane, než bychom mohli říct něco o limitě f.

Nicméně tak, jak je formulována, může být věta užitečná k důkazu, že nějaká limita neexistuje.

Příklad: Ukážeme, že sin(x) nemá limitu v nekonečnu.

Uvažujme dvě poslounpsti, x_n = πn a y_n = π/2 + 2πn. Obě jdou do nekonečna. Co dostaneme, když je dosadíme do sinu?

sin(x_n) = 0 pro každé n, proto sin(x_n)→0. Na druhou stranu, sin(y_n) = 1 pro každé n, proto sin( y_n)→1.

Pokud by tedy měl sinus limitu v nekonečnu, pak by podle poslední věty musely jít jak {sin(x_n)}, tak {sin( y_n)} k této limitě. Protože ale jdou k rozdílým číslům, nemůže existovat limita sinu v nekonečnu.

Více se o spojitosti mezi funkcemi a posloupnostmi dozvíte v sekci Posloupnosti a funkce v části Posloupnosti - Teorie - Limita.

Limita a srovnání
Zpět na Teorie - Limita