Příklad: Najděte globální extrémy funkce

f (x) = x² − 8|x − 1| + 8

na intervalu I = ⟨−1,6⟩.

Řešení: Abychom našli globální extrémy na uzavřeném omezeném intervalu, porovnáme hodnoty f v podezřelých bodech. Jsou dva druhy kandidátů: krajní body (zde −1 a 6) a kritické body dané funkce.

Jsou dva druhy kritických bodů: Body definičního oboru, kde derivace neexistuje, a body, kde je derivace nulová. Začneme tedy tím, že najdeme derivaci dané funkce. Vidíme, že obsahuje absolutní hodnotu, což znamená, že derivaci neumíme najít přímo. Nejprve se musíme zbavit absolutní hodnoty tím, že funkci přepíšeme jako funkci rozpisem.

Derivaci takové funkce můžeme hledat pomocí obvyklých pravidel pouze na otevřených intervalech z její definice.

Jak je tomu s derivací v bodě 1? Rozhodnout, zda tam derivace je, můžeme pomocí jednostranných derivací (viz poznámka níže), ale není to tady vlastně nutné. My jen hledáme podezřelé body, kde může být nějaký extrém, a bod x = 1 je dostatečně podezřelý, zahrneme jej mezi kandidáty (leží v naší množině I). Další kandidáty najdeme tím, že se podíváme po nulových bodech derivace.

Číslo x = 4 splňuje x > 1, takže leží v oblasti, kde příslušný vzorec dává f ′, a je to tedy opravdu nulový bod derivace. Podobně je x = −4 platným nulovým bodem. Nás ale zajímá jen to, co se děje na množině I, kam −4 nepatří, a tak tento bod budeme ignorovat.

Máme 4 kandidáty na globální extrémy: −1, 1, 4, 6. Porovnáme hodnoty:

f (−1) = −7,
f (1) = 9,
f (4) = 0,
f (6) = 4.

Vidíme, jaká je největší a nejmenší hodnota, a usoudíme, že max _I ( f ) = f (1) = 9 a min _I ( f ) = f (−1) = −7.

Poznámka: Pokud bychom chtěli vědět, jestli je v bodě 1 derivace, tak nejjednodušší je najít jednostranné derivace v 1 pomocí limity, viz příslušná věta v sekci Derivace a limita v části Teorie - Věta o střední hodnotě. Počítali bychom

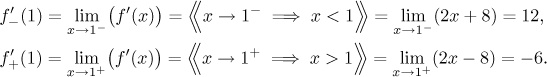
Protože ty jednostranné derivace nesouhlasí, tak neexistuje derivace f v 1.

Další příklad
Zpět na Řešené příklady - Aplikace