Riemannův integrál

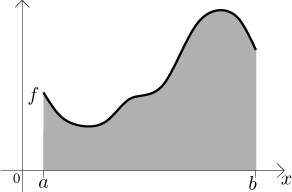
Motivace: Nechť f je funkce definovaná na uzavřeném intervalu ⟨a,b⟩. Pro jednoduchost si představíme, že f je spojitá a kladná. Pak má smysl uvažovat oblast mezi osou x a grafem f.

Pokud se nám nějak podaří najít obsah této oblasti, budeme tomu číslu říkat určitý integrál z f od a do b.

Určení obsahu se dá zkusit mnoha způsoby, ale podle toho, jaké má funkce f vlastnosti, to může být velmi těžké či dokonce nemožné. My zde použijeme Riemannův přístup. Je založen na jednoduchém postřehu, že snadno spočítáme obsah obdélníka. Budeme se tedy snažit aproximovat oblast pod grafem f pomocí vhodných obdélníků.

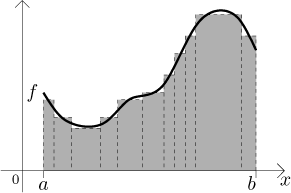
Z obrázku se zdá, že pokud bychom udělali ty obdélníky extrémně úzké, byla by chyba aproximace velice malá. Pokud tedy budeme zkoušet užší a užší obdélníky, při troše štěstí budou tyto aproximované obsahy konvergovat k nějakému číslu, jmenovitě ke skutečnému obsahu oblasti pod grafem f. Tento postup selže, pokud se při zužování obdélníků nebudou zmenšovat chyby aproximace; toto závisí na tvaru f, opravdu divoké funkce vedou k podivným oblastem a někdy ani nemá smysl mluvit o jejich obsahu.

Teď se pokusíme naše úvahy udělat přesně.

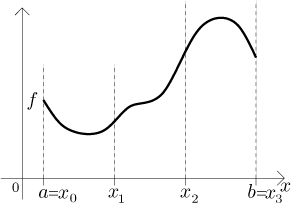
Šířky obdélníků jsou určeny, když interval ⟨a,b⟩ rozdělíme na menší části. Používáme k tomu pojmu dělení:

Definice.
Uvažujme uzavřený interval ⟨a,b⟩. Dělením intervalu ⟨a,b⟩ rozumíme libovolnou konečnou množinu P={x₀, x₁,..., x_N} bodů z ⟨a,b⟩ splňujících podmínku a = x₀ < x₁ < . . . < x_N = b.

Uvažujme nějakou omezenou funkci f definovanou na intervalu ⟨a,b⟩. Když zvolíme nějaké dělení, interval ⟨a,b⟩ se rozpadne na N částí, které určí svislé strany aproximujících obdélníků:

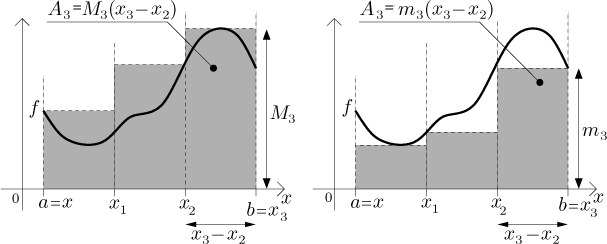
Teď se musíme rozhodnout, jaké budou jejich výšky. Na to je několik metod, zde použijeme tu, se kterou se nejjednodušeji pracuje. Abychom se pojistili, zkusíme prostě ty největší a nejmenší možné (a rozumné) obdélníky, čímž dostaneme horní součet a dolní součet:

Definice.
Nechť f je omezená funkce definovaná na uzavřeném intervalu ⟨a,b⟩. Je-li dáno dělení P intervalu ⟨a,b⟩, pro k = 1,...,N označme

Pak definujeme horní součet příslušný dělení P vzorcem

Podobně definujeme dolní součet příslušný dělení P:

Čtenář by měl vědět, že značení U a L zde použité není standardní. V české literatuře se pro součty používá různých značení (například S podtržené nahoře a dole či znak integrálku s čárkou nahoře a dole atd.), "správné" značení tedy neexistuje. Zde zvolené označení jsme vybrali s ohledem na rozšířené symboly v anglické literatuře (upper/lower sum), už proto, aby čtenář nebyl zmaten, pokud se rozhodne podívat do anglické verze těchto stránek.

Povšimněte si, že ona suprema a infima vždy existují a jsou konečná díky omezenosti funkce f, takže součty jsou dobře definovány. V obou případech vlastně sčítáme obsahy obdélníků. Jejich základny jsou dány dělením, výšky pak supremem či infimem f v jednotlivých obdélnících.

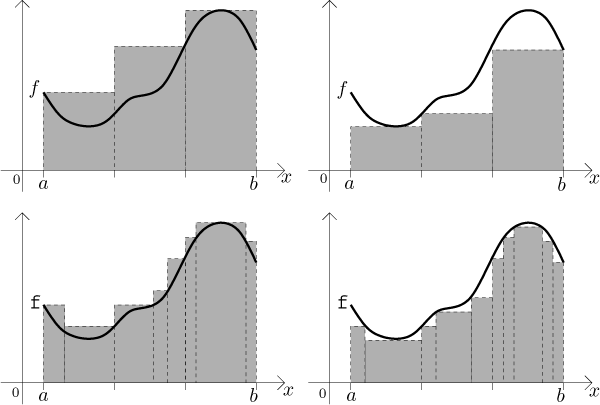
Horní i dolní součet je znázorněn na následujícím obrázku. Šrafovaná plocha nalevo je horní součet, napravo dolní součet. V grafech jsme také označili některé výrazy použité při výpočtu obsahu třetího obdélníka.

Pokud označíme skutečný obsah oblasti pod grafem f jako A (doufajíce, že obsah existuje), pak se z obrázku zdá zřejmé, že

Abychom našli hodnotu A, budeme měnit obdélníky takovým způsobem, aby se horní součet zmenšoval a dolní součet zvětšoval, dokud se nebudou skoro rovnat. Protože skutečný obsah je vždy mezi horním a dolním součtem, rovnost součtů znamená, že jsme určili A. Změny obdélníků budou mít formu jejich zužování. U užších obdélníků je i menší chyba aproximace, což znamená, že se bude horní součet zmenšovat (a tedy přibližovat k A) a dolní součet se bude zvětšovat (a přibližovat k A). Srovnejte na následujícím obrázku chybu aproximace horního a dolního součtu při zjemnění dělení.

Výhodou přístupu použitím horních a dolních součtů je, že nás nemusí zajímat, jak se vlastně to zužování obdélníků přesně dělá, všechny detaily jsou chytře schovány v následující definici. Bohužel, tento Riemannův přístup přes obdélníky funguje, jen pokud je funkce f dostatečně pěkná, říkáme Riemannovsky integrovatelná. Přesně řečeno:

Definice.
Nechť f je omezená funkce definovaná na uzavřeném intervalu ⟨a,b⟩. Řekneme, že f je Riemannovsky integrovatelná na ⟨a,b⟩, jestliže infimum horních součtů přes všechna dělení intervalu ⟨a,b⟩ je rovno supremu dolních součtů přes všechna dělení ⟨a,b⟩.

Pak definujeme Riemannův určitý integrál funkce f od a do b jako

Obvykle říkáme prostě Riemannův integrál, rozumí se, že se tím míní určitý integrál. Protože pro Riemannovsky integrovatelné funkce se infimum horních součtů rovná supremu dolních součtů, mohli jsme toho druhého rovněž použít k definici Riemannova integrálu.

Tomu hadovitému tvaru se říká integrační symbol, je to vlastně prodloužené S (jako suma). Integrované funkci se někdy říká integrand. Máme zde dolní mez a a horní mez b, které určují integrační interval ⟨a,b⟩. Proměnné x se říká integrační proměnná a vlastně na ní nezáleží. Protože Riemannův integrál je chápán jako obsah pod grafem f, jediná důležitá informace je tvar grafu. Pokud se tedy rozhodneme použít ve témže vzorci jinou proměnnou, tvar grafu a tedy i integrál zůstanou stejné. Takže například

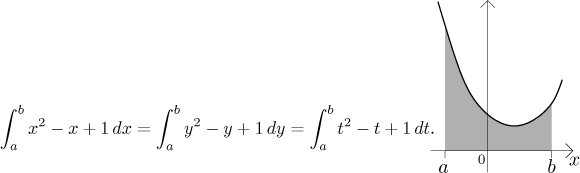
Zdá se to zřejmé, plocha pod tímtéž kouskem dané paraboly je vždy stejná, ať už k vodorovné ose připíšeme jakékoliv písmenko.

Symbol dx je diferenciál proměnné x (viz např. Derivace - Teorie - Úvod - Leibnizovo značení) a zde hraje spíš jen symbolickou roli. Je to nedílná součást značení Riemannova integrálu, takže je důležité jej nevynechat. Obzvláště kritické je to v případě, že integrovaná funkce má několik proměnných (či nějaké parametry), diferenciál pak jasně ukáže, které písmenko ve funkci se použije jako proměnná při integraci. Zatímco vynechání diferenciálu se silně nedoporučuje, v obecných vzorcích lidé často píší jen f namísto f (x) k ušetření času; správná proměnná je stejně jasná z diferenciálu. I my to tady občas uděláme, ale v důležitých vzorcích se pokusíme psát věci pořádně.

Podrobnější vysvětlení významu integrálních symbolů (které není matematicky korektní, ale usnadní pochopení) lze najít zde.

V definici jsme použili menší mez (levý konec intervalu) jako dolní mez integrálu. Někdy ovšem potřebujeme "integrovat pozpátku", od b k a. Často prostě jen potřebujeme napsat integrál, aniž bychom se museli zabývat pořadím mezí, takže potřebujeme obecnější definici. Vypadá takto: Nechť a < b. Definujeme

Když teď umíme integrovat s libovolným pořadím mezí, tato formulka se stává obecným vzorcem: Můžeme kdykoliv prohodit integrační meze, pokud zároveň přidáme před integrál mínus.

Příklad: Vyšetříme integrál

Měli bychom se rozhodnout pro nějaká dělení, která povedou ke stále užším a užším kouskům, doufaje, že příslušné horní a dolní součty se budou přibližovat, až splynou. Pokud nemáme nějaký specifický důvod postupovat jinak, bývá většinou dobré prostě zkusit rovnoměrné rozdělení, neboli pro dané přirozené číslo N rozdělit interval ⟨2,4⟩ na N stejně dlouhých částí. Dostaneme tak následující dělení (přesvědčte se sami)

Teď bychom měli najít jednotlivá suprema a infima pro součty, ale to je zde lehké přímo z obrázku:

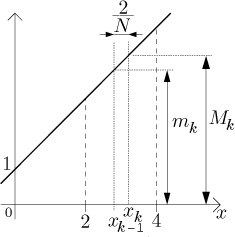
Najdeme tedy horní a dolní součet:

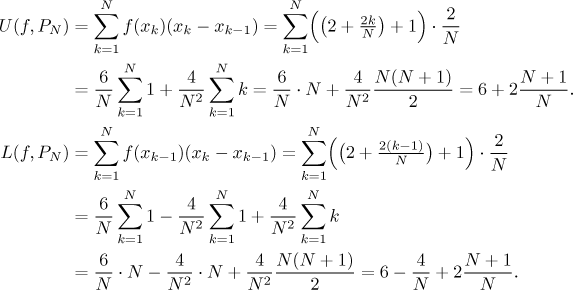
Protože jsme použili velmi speciálních dělení, nedá se obecně čekat, že by vedly k hledanému obsahu (v jeho definici jsme totiž zkoumali všechna rozdělení). Nicméně zde máme velice pěknou funkci, a tak se ukáže, že když pošleme N do nekonečna, součty dobře aproximují daný obsah. Pokud chceme být přesní podle definice, musíme být trochu opatrnější:

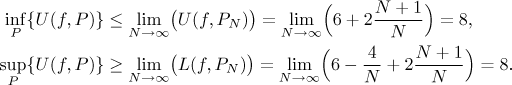
Proto

a tedy

Ukázali jsme, že funkce f (x) = x + 1 je Riemannovsky integrovatelná na ⟨2,4⟩ a

Je lehké ověřit správnost odpovědi, prostě se z obrázku spočítá obsah lichoběžníka podle příslušného vzorečku.

Tento výpočet nebyl zrovna snadný, a to jsme ještě měli štěstí a pamatovali si vzoreček pro součet prvních N přirozených čísel. U více komplikovaných funkcí je často nemožné najít explicitní vzorec pro horní a dolní součet. Proto obvyukle používáme jiné nástroje k nalezení Riemannova integrálu (viz Základní věta integrálního počtu).

V našich obrázcích jsme vždy měli kladné funkce; Riemannův integrál je pak roven geometrickému obsahu obrazce mezi grafem f a osou x. Co když máme zápornou funkci? Protože hodnoty f určují výšky obdélníků, dostaneme plochy, ale se záporným znaménkem. Takže pro záporné funkce je jejich Riemannův integrál roven mínus geometrický obsah oblasti mezi grafem f a osou x.

Pro obecnou funkci je Riemannův integrál roven matematickému obsahu oblasti mezi grafem f a osou x, což je geometrický obsah částí, které jsou nad osou x, minus geometrický obsah částí pod osou x. Například v následujícím obrázku jsme písmenem A s indexy 1,2,3 označili geometrické obsahy jednotlivých částí:

To je velmi důležitá otázka. Pro naše účely je nejdůležitějším faktem toto:

Věta.
Každá funkce spojitá na uzavřeném intervalu je tam Riemannovsky integrovatelná.

Tento příklad ukazuje, že pokud má funkce někde skokovou nespojitost, může být ještě pořád Riemannovsky integrovatelná. Na druhou stranu, příklad Dirichletovy funkce ukazuje, že pokud je bodů nespojitosti příliš, funkce už Riemannovsky integrovatelná není. Ve skutečnosti platí, že funkce je Riemannovsky integrovatelná, právě když jejích bodů nespojitosti není příliš mnoho. Přesnější informace je zde.

To, že Riemannovská integrabilita není ohrožena konečným počtem nespojitostí, má něco společného s faktem, že hodnota Riemannova integrálu není ovlivněna změnou integrované funkce v konečném počtu bodů. Přesně řečeno, předpokládejme, že f je Riemannovsky integrovatelná na intervalu ⟨a,b⟩. Pokud je g funkce, která je rovna f na ⟨a,b⟩ s výjimkou konečného počtu bodů, pak g je také Riemannovsky integrovatelná na ⟨a,b⟩ a integrály f a g jsou shodné.

Abyste měli představu, proč by tohle mohlo platit, podívejte se na následující obrázek, kde jsme obdrželi g přičtením 1 k funkci f v bodě c.

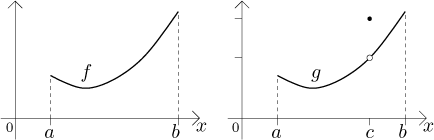
Oblast pod grafem g je vlastně oblast pod grafem f plus přidaná svislá čárka v místě, kde se f změnilo v g. Protože tato úsečka má tloušťku jednoho bodu, což je nula, je také její obsah nulový a proto není pod g žádná plocha navíc.

Stať zakončíme užitečným faktem:

Věta.
Každá funkce monotónní na uzavřeném intervalu je tam Riemannovsky integrovatelná.

Vlastnosti Riemannova integrálu
Zpět na Teorie - Úvod do integrace