Příklad: Vyšetřete konvergenci následující řady funkcí:

Řešení: Nejprve se podíváme na bodovou konvergenci. Budeme považovat x za parametr a vyšetříme konvergenci výsledné řady reálných čísel. Protože je hyperbolický kosinus vždy kladný, má daná řada nezáporné členy a my tedy můžeme použít k určení její konvergence (která je zde stejná jako absolutní konvergence) vhodné testy.

Jaké testy vypadají dobře? Dělat k-tou odmocninu z hyperbolického kosinu nevypadá moc přitažlivě, což takhle podílové kritérium?

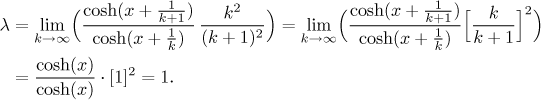
Toto kritérium tedy dopadlo neurčitě. Jaké jiné testy se dají použít? Jediná rozumná možnost je limitní srovnání. Vidíme, že pro velká k je čitatel v zásadě roven cosh(x), což je konstanta (teď bereme x jako parametr), a tak je to možné vytáhnout z řady. Proto si tipneme, že se naše řada chová jako řada s 1/k². Tento odhad je nutno potvrdit.

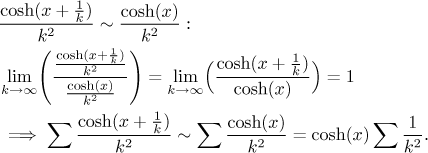
Protože řada napravo konverguje (viz p-test), také řada nalevo konverguje. Všimněte si, že tato konvergence nezáleží na x.

Závěr: Daná řada konverguje (absolutně) na celé reálné ose (což je tedy také obor (absolutní) konvergence této řady).

Jak je na tom stejnoměrná konvergence? Protože neznáme součet dané řady, nemůžeme použít přímé metody. Použité srovnání ale naznačuje, že by Weierstrassovo kritérium mělo dobře fungovat na omezených množinách. A opravdu, zvolme nějaké A < B a uvažujme množinu M=⟨A,B⟩. Pomocí toho, že hyperbolický kosinus je sudý a rostoucí na (0,∞), můžeme pro x z M odhadovat

Proto

Jelikož řada ∑ a_k konverguje (viz výše), daná funkční řada konverguje stejnoměrně na M.

Závěr: Daná řada konverguje stejnoměrně na libovolném omezeném a uzavřeném intervalu.

Další příklad
Zpět na Řešené příklady - Řady funkcí